Question

Катеты прямоугольного треугольника АBC равны 3 и 4. Расстояние между плоскостью, проходящей через гипотенузу треугольника, и вершиной прямого угла равно 1,2 см. Найдите угол между треугольниками и плоскостью. (можно пж с рисунком)

Answer 1

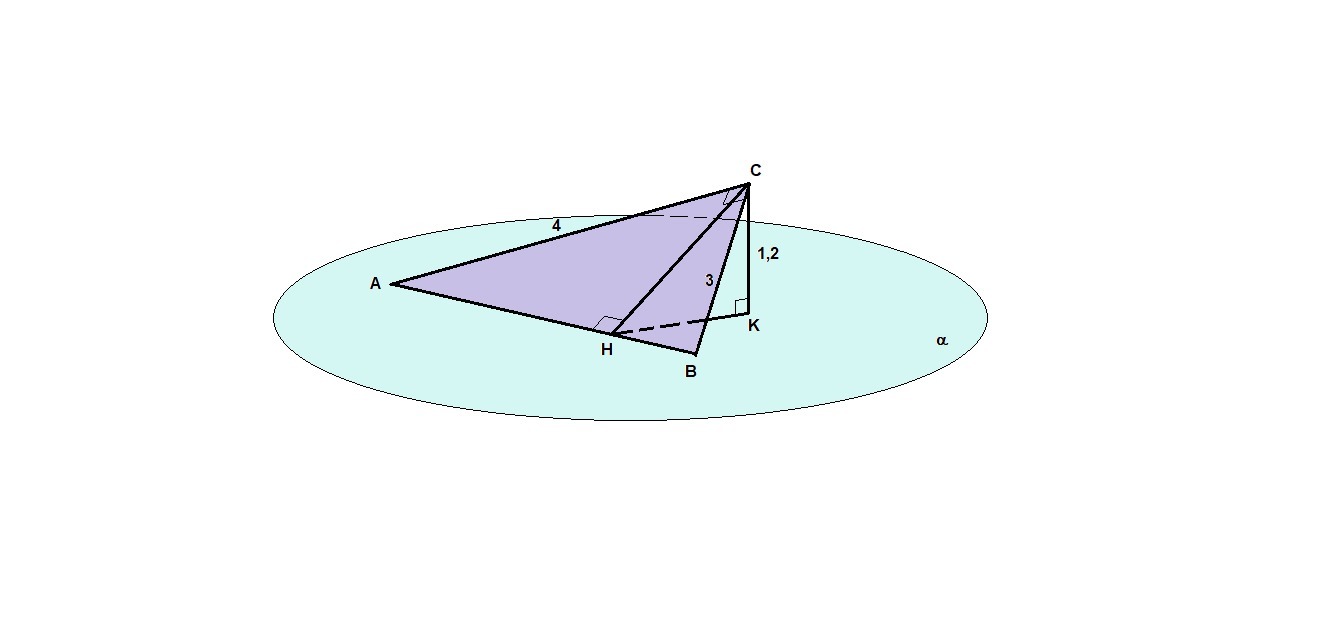
СК - перпендикуляр к плоскости α, проходящей через гипотенузу треугольника. Тогда СК = 1,2 см - расстояние от вершины С до плоскости.

СН - высота треугольника, проведенная к гипотенузе.

СН ⊥ АВ, КН - проекция СН на плоскость α, тогда и КН ⊥ АВ по теореме, обратной теореме о трех перпендикулярах.

∠СНК - линейный угол двугранного угла между плоскостью треугольника и плоскостью α - искомый.

ΔАВС прямоугольный, с катетами 3 и 4, египетский, значит

АВ = 5 см.

СН = АС·ВС / АВ = 3 · 4 / 5 = 12/5 = 2,4 см

ΔСКН: ∠СКН = 90°

           sin∠CHK = CK / CH = 1,2 / 2,4 = 1/2

∠CHK = 30°