Предмет: Геометрия,
автор: liza3430
ПОМОГИТЕ! СРОЧНО ОЧЕНЬ ОЧЕНЬ НАДО!!!
Приложения:
Ответы
Автор ответа:
2
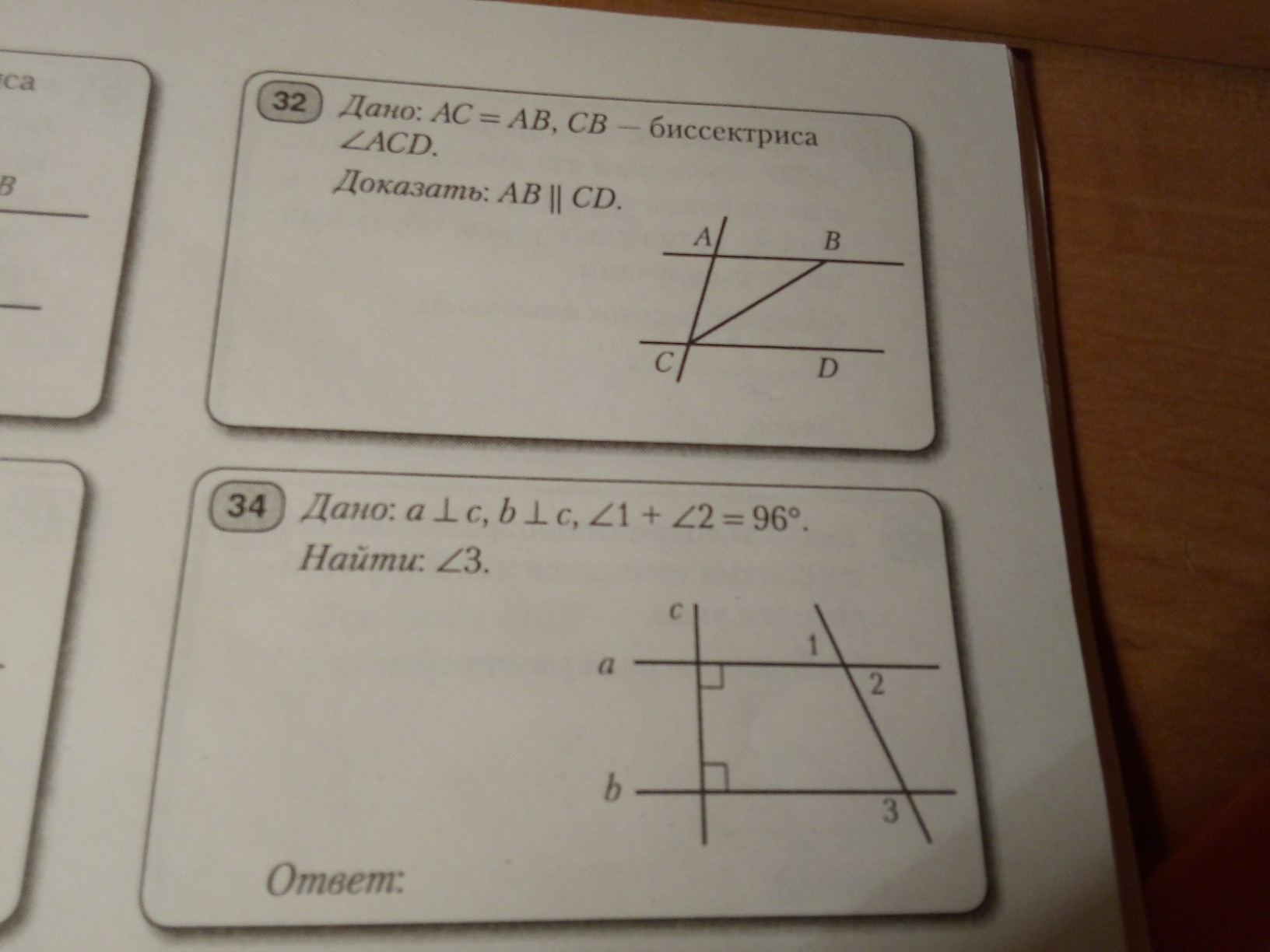
Так как ав = ас ⇒ Δ авс = равнобедренный ⇒ угол Асв = углу Авс
Так как СВ это биссектриса и она делит угол на два равных то угол АСВ = углу ВСД
А так как угол ВСД = углу АСВ (когда тот равен еще и углу АВС), можем говорить что угол ВСД = углу АВС
Рассмотрим две прямые, которые надо доказать АВ и СД, у них есть секущая СВ, угол АВС = углу ВСД и при этом они являются накрест лежащими углами при секущей СВ, а если накрест лежащие углы при секущей равны, значит те прямые буду параллельными , что и требовалось доказать
Если помогла, сделай пожалуйста ответ лучшим
Автор ответа:
1
Этот треугольник равнобедренный, так, как у него АВ и ВС равны..!
ВС - биссектриса, она делит угол на равные части, поэтому АСВ равно ВСD!
Взглянем на прямые, которые нужно будет доказать, это АВ и СD, у них присутствует секущая ВС, а угол АСВ равен углу ВСD, при чём они расположены накрест лежащими при секущей BC, а если углы при секущей будут равны, то они будут параллельны друг другу...
ВС - биссектриса, она делит угол на равные части, поэтому АСВ равно ВСD!
Взглянем на прямые, которые нужно будет доказать, это АВ и СD, у них присутствует секущая ВС, а угол АСВ равен углу ВСD, при чём они расположены накрест лежащими при секущей BC, а если углы при секущей будут равны, то они будут параллельны друг другу...
Похожие вопросы
Предмет: Английский язык,
автор: aizerekairat6
Предмет: Математика,
автор: djjeucifkjdioejd
Предмет: Математика,
автор: strelnikovaalina29
Предмет: Математика,
автор: Лиза1111115682
Предмет: Литература,
автор: tatoshka098