Предмет: Алгебра,
автор: kuzyaev01
Найдите наименьшее значение функции 
На отрезке [-5;6] Если предмет выбран неверно то удалите моё задание и верните балы как можно скорее и пожалуйста помогите с заданием
Ответы
Автор ответа:
4
решение на фотографии
Приложения:
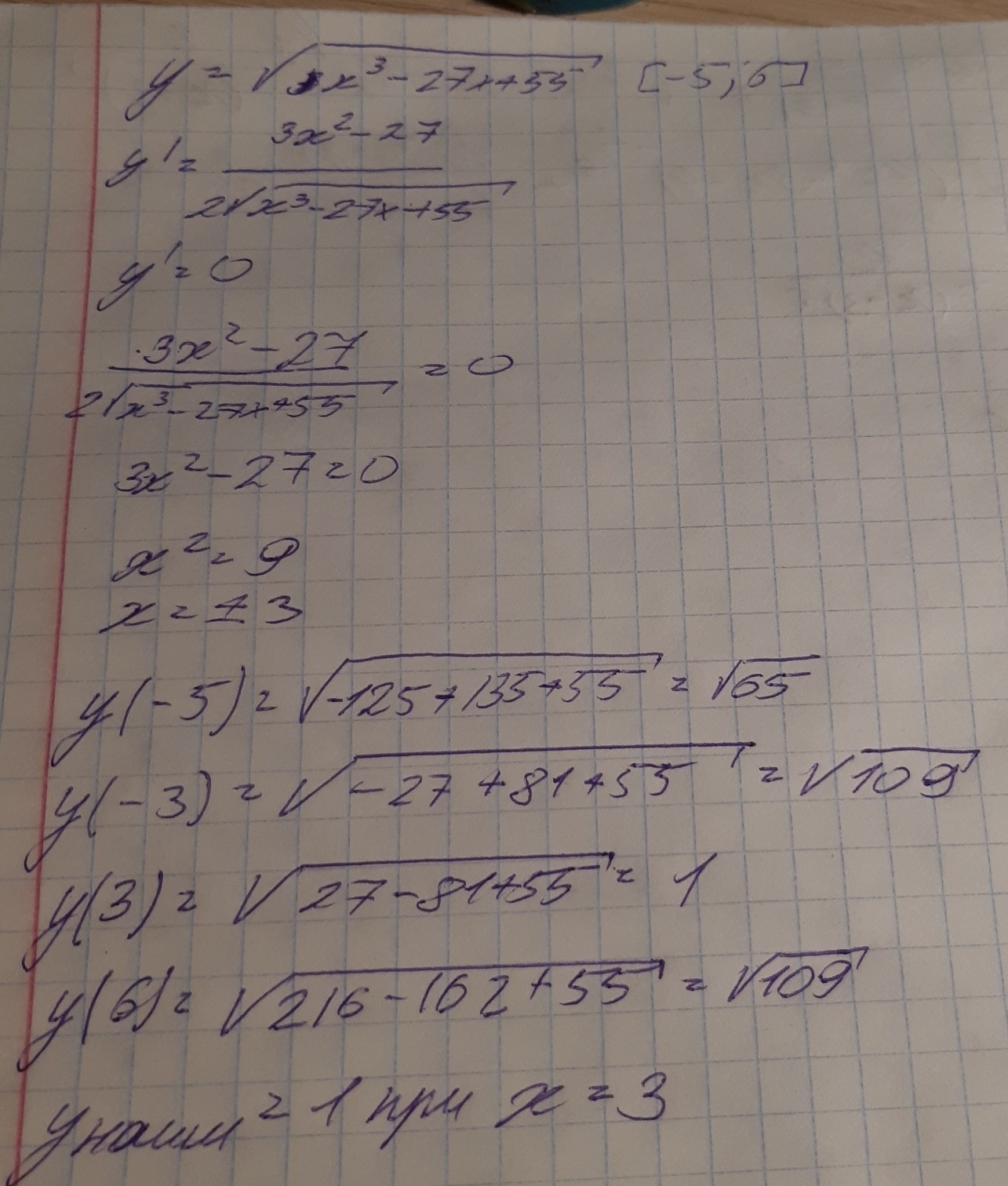
Автор ответа:
7
Ответ: 1
Похожие вопросы
Предмет: Русский язык,
автор: qudretmustafayev9
Предмет: Алгебра,
автор: 5kripka
Предмет: Английский язык,
автор: marimati
Предмет: Математика,
автор: Адема2004
Предмет: Математика,
автор: Аноним