Question

Дам 30 баллов!!
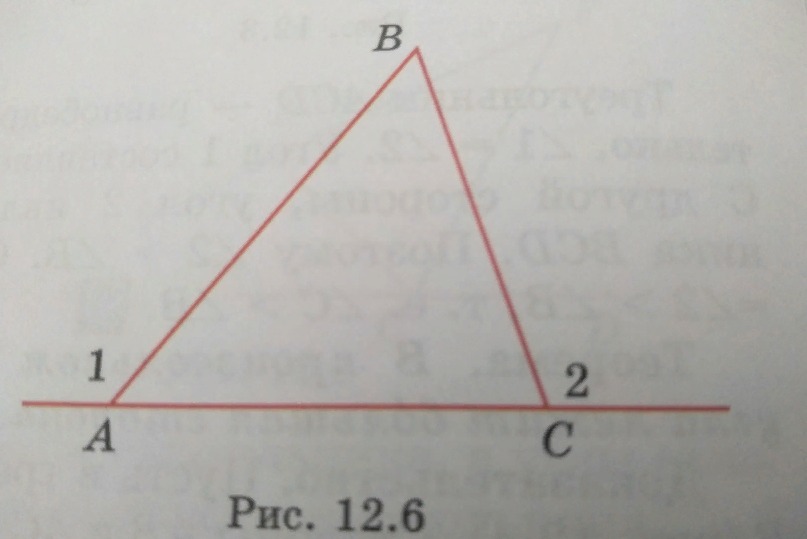
На рисунке 12.6 AB больше BC.Докажите что угол 1 больше угла 2.

Answer 1

По теореме синусов:

$\frac{AB}{\sin{C}}=\frac{BC}{\sin{A}}\\\frac{\sin{C}}{\sin{A}}=\frac{AB}{BC}>1\longrightarrow \sin{C}>\sin{A}$

Т.к. углы A и C острые, т.е. меньше π / 2, а функция синус на отрезке [0; π / 2] возрастающая, то из неравенства sin(C) > sin(A) следует, что и ∠C > ∠A.

∠1 = 180° - ∠A > 180 - ∠C = ∠2, что и требовалось доказать.