выполните действия номер 31.2
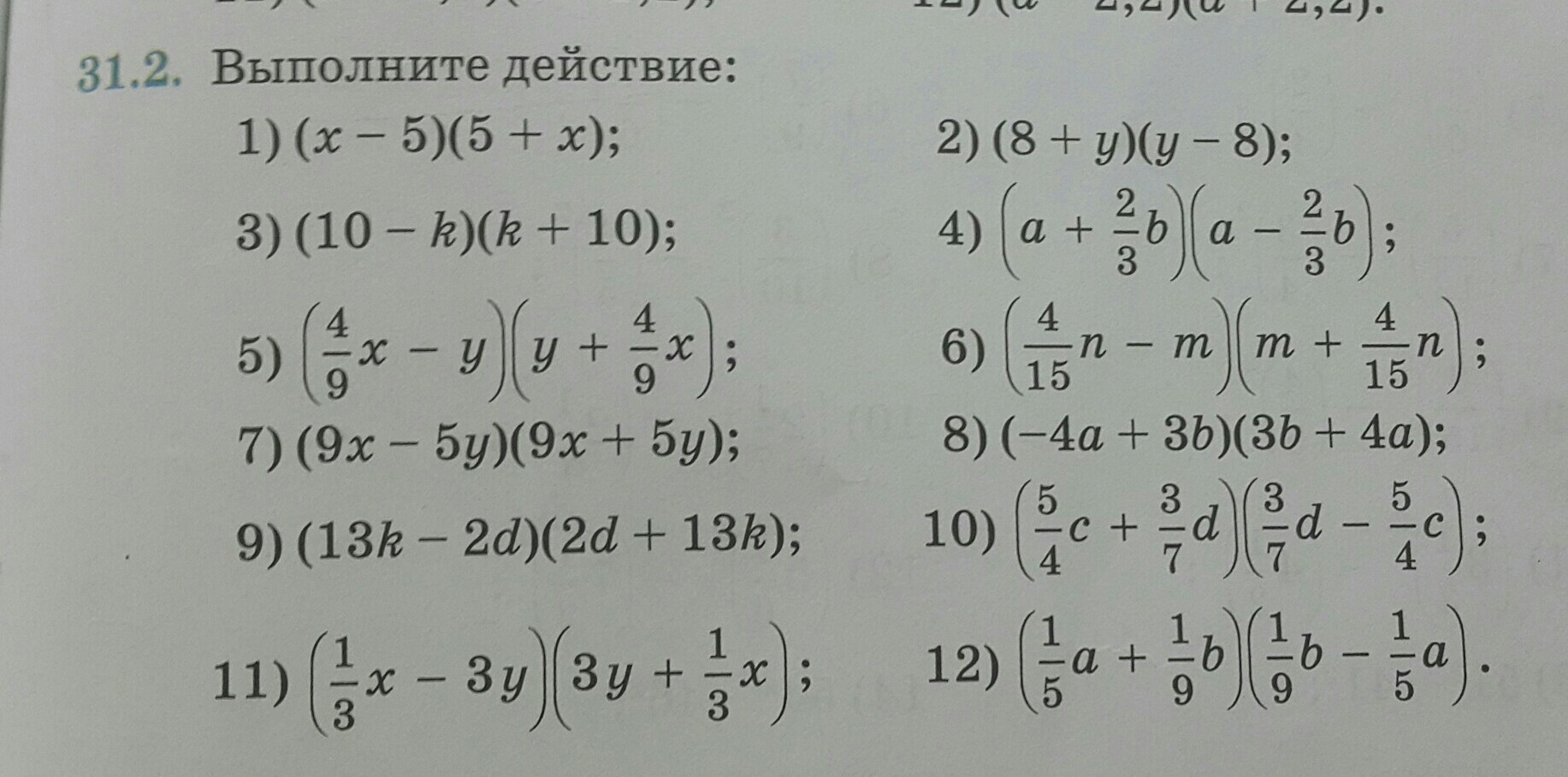
Ответы
Все задания на применение формулы сокращенного умножения
(a - b)(a + b) = a² - b².
1) (x - 5)(5 + x) = (x - 5)(x + 5) = x² - 5² = x² - 25;
2) (8 + y)(y - 8) = (y - 8)(y + 8) = y² - 8² = y² - 64;
3) (10 - k)(k + 10) = (10 - k)(10 + k) = 10² - k² = 100 - k²;
4) (a + 2/3 · b)(a - 2/3 · b) = a² - (2/3 · b)² = a² - 4/9 · b²;
5) (4/9 · x - y)(y + 4/9 · x) = (4/9 · x)² - y² = 16/81 · x² - y²;
6) (4/15 · n - m)(m + 4/15 · n) = (4/15 · n)² - m² = 16/225 · n² - m²;
7) (9x - 5y)(9x + 5y) = (9x)² - (5y)² = 81x² - 25y²;
8) (-4a + 3b)(3b + 4a) = (3b - 4a)(3b + 4a) = (3b)² - (4a)² = 9b² - 16a²;
9) (13k - 2d)(2d + 13k) = (13k)² - (2d)² = 169k² - 4d²;
10) (5/4 · c + 3/7 · d)(3/7 · d - 5/4 · c) = (3/7 · d - 5/4 · c)(3/7 · d + 5/4 · c) =
= (3/7 · d)² - (5/4 · c)² = 9/49 · d² - 25/16 · c² = 9/49 · d² - 1 целая 9/16 · с²;
11) (1/3 · х - 3у)(3у + 1/3 · х) = (1/3 · х)² - (3у)² = 1/9 · х² - 9у²;
12) (1/5 · a + 1/9 · b)(1/9 · b - 1/5 · a) = (1/9 · b)² - (1/5 · a)² = 1/81 · b² - 1/25 · a².