Предмет: Алгебра,
автор: tordedd
пожалуйста, помогите с математикой. 10 класс
большое спасибо всем, кто откликнется
Приложения:
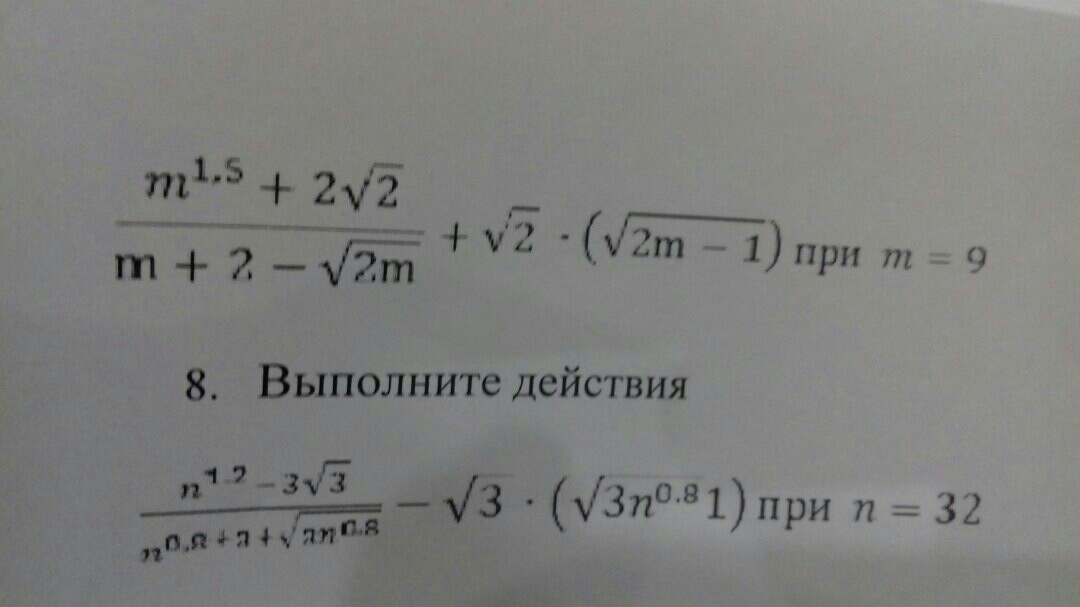

Ответы
Автор ответа:
1
Сначала приведём обе части выражения к общему знаменателю. Для этого надо домножить и разделить второе слагаемое на знаменатель первой дроби. Получим:
Вынесем корень из двух за скобку в числителе:
Раскроем скобки в числителе:
Выражение примет этот вид:
Переведя корни с неизвестной в степени 0.5, после приведения всех подобных получаем упрощённый вид выражения:
Подставив , получим:
По тому же принципу решается и выражение из задачи 8.
tordedd:
спасибо Вам огромное ♡
Пожалуйста) Неравенства оставлю кому-нибудь ещё.
Автор ответа:
0
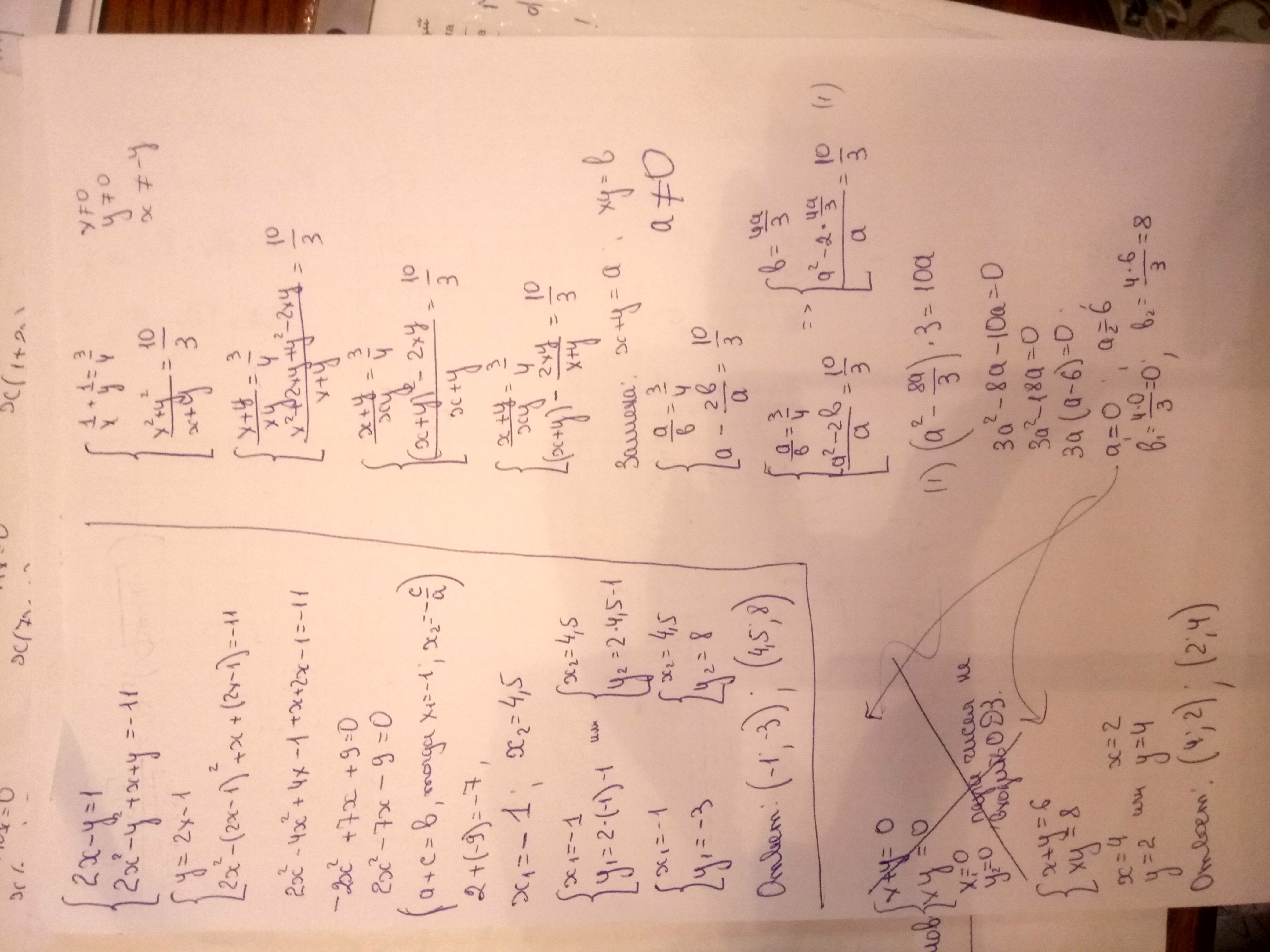
Это системы уравнений с 2мя неизвестными. Решение задания Приложено. Добавила решение первого. Там опечатка в условии. И видим, что нужно использовать формулу сумма кубов.
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: wwwcatsag
Предмет: Биология,
автор: yamidekedasaii
Предмет: Математика,
автор: irinadavidko2004
Предмет: Математика,
автор: Андрей1Руфер
Предмет: Литература,
автор: harnatalya