Предмет: Геометрия,
автор: ilia1391
в равнобедренном треугольнике ABC с основанием AC, медианы AK и CM пересекаются в точке O. Докажите, что угол KAC=углу MCA
Ответы
Автор ответа:
28
В равнобедренном треугольнике ABC рассмотрим два треугольника KAC и MCA. Треугольник KAC равен треугольнику MCA по двум сторонам и углу между ними, а именно:
1). Сторона AC - общая;
2). MA=KC, так как:
AB=BC, ведь треугольник ABC - равнобедренный, а MA=1/2*AB (т. M - середина AB, т.к. MC - медиана), KC=1/2*BC (т. K - середина BC, т.к. KA - медиана), значит MA=KC;
3). ∠BAC=∠BCA, т.к. треугольник ABC - равнобедренный.
Из равенства треугольников KAC и MCA следует равенство соответственных элементов, а значит ∠KAC=∠MCA, что и требовалось доказать.
Приложения:
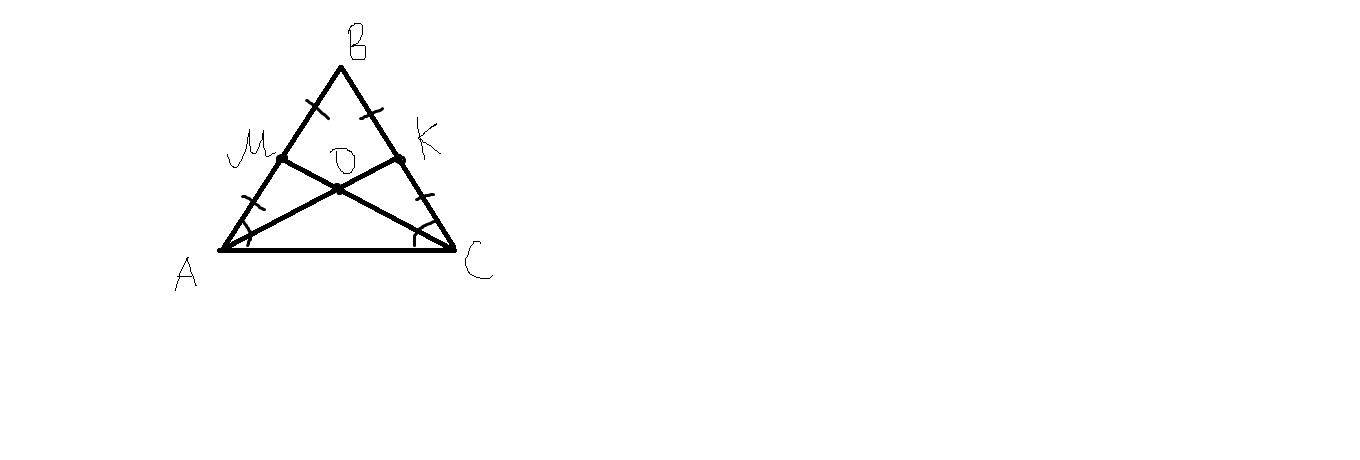
Похожие вопросы
Предмет: Математика,
автор: osedova012
Предмет: Алгебра,
автор: catsarethebest
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: artalina5
Предмет: География,
автор: ника1350