Предмет: Алгебра,
автор: mboroli
СРОЧНО, ПОЖАЛУЙСТА! Найти экстремумы и точки перегиба функции y=x^3+9x^2+15x-25
Постройте график, пожалуйста!!!
Ответы
Автор ответа:
0
Ответь в фото..............
Приложения:
Автор ответа:
0
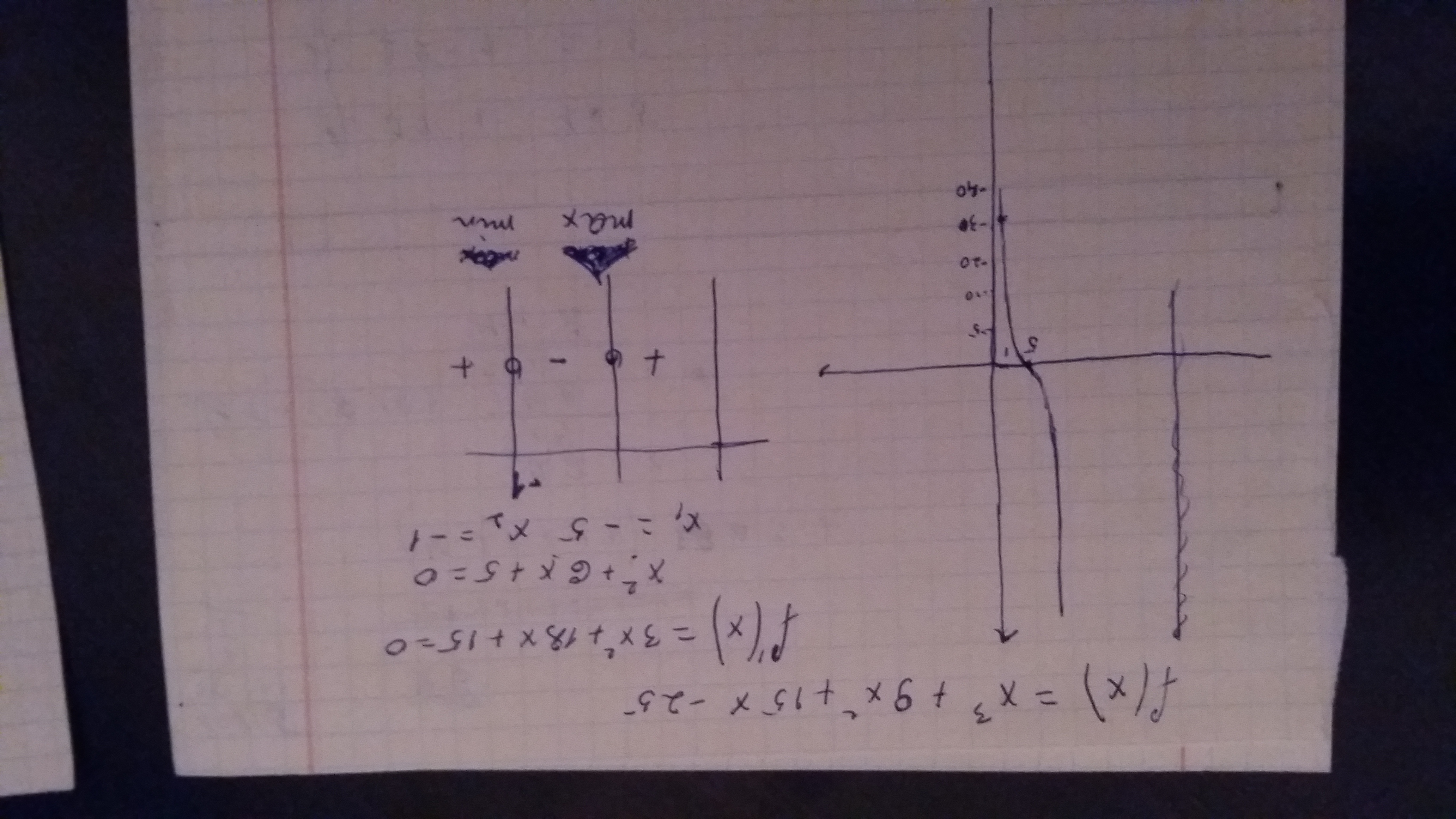
1) Найдём производную: y' = 3x² + 18x + 15; Решим уравнение: 3x² + 18x + 15 = 0, x + 6x + 5 = 0, по теореме Виета: x₁ + x₂ = - 6, x₁ · x₂ = 5 ⇒
x₁ = - 1; x₂ =- 5 ⇒ на промежутке ( - ∞, - 5) функция возрастает;
на ( -5, - 1) убывает и на ( - 1, + ∞) возрастает, таким образом ( -5) - точка максимума, (-1) - точка минимума.
Вычислим: y (- 5) = (-5)³ + 9 · (-5)² + 15 · (-5) - 25 = 0; y (-1) = (-1)³ + 9 · (-1)² + 15 · (-1) - 25 = - 32
Итак: Строим график - От ( +∞) до точки ( - 5; 0) функция возрастает; От точки ( -5; 0) до точки (- 1; - 32) функция убывает и от точки ( -1; - 32)
до (-∞) возрастает.
Точки перегиба: ( -5; 0) и (- 1; - 32)
Аноним:
вы точки экстремума не путайте с точками перегиба.
точка перегиба это вторая производная
Похожие вопросы
Предмет: Английский язык,
автор: zinolovdenalbina
Предмет: Русский язык,
автор: prorivalena
Предмет: Физика,
автор: ademuusha
Предмет: Литература,
автор: art62
Предмет: Литература,
автор: lian4