Предмет: Алгебра, автор: Алексей55578678

(решение есть, но нужно объяснить, оч легкое) вот как можно найти корни, если дискриминант не получается?? Кроме теоремы виета есть что-нибудь еще?Просто в решение какая-то дичь написано, не понятно как они додулись.

Приложения:

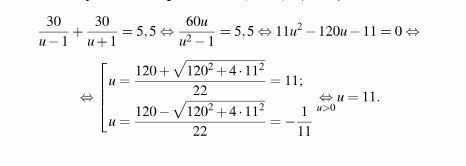
Ответы

Автор ответа: vavdovina55

под корнем как раз дискриминант - он равен 14884 и если извлечь корень - будет 122

LFP: для этого уравнения т.Виета сложно применить--оно НЕ приведенное (старший коэффициент не=1)) а еще есть "метод переброски" (мне оч.!! понравился)) домножить обе части уравнения на (а=11) старший коэфф. и получим другое кв.уравнение, в котором уже можно и по т.Виета: (11u)^2 - 120*(11u) - 121 = 0 по т.Виета корни устно (!!) 121 и (-1) и получим: 11u = 121 ---> u=11 (u не равно -1)

LFP: опечатка: получим: 11u = 121 ---> u=11 и 11u = -1 ---> u=-1/11

LFP: почитайте про "метод переброски" !! реально почти все кв.ур. можно устно решать (если потренироваться)))

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Геометрия, автор: arinaaaaaaa0000

найдите х помогите пожалуйста

5 лет назад

Предмет: Математика, автор: superdgoyt23

5 класс

Подберите пару чисел а и б, удовлетворяющую равенству: (a + 2,1)=3,2+b

a) a = 0,5 ; b=0
б) a=1 ; b=1
в) a=0 ; b=1
г) a = 1,5 ; b=2

СКАЖИТЕ КАКО1 ИЗ ЭТИХ ВАРИАНТОВ??? ДАМ 25 БАЛЛОВ

5 лет назад

Предмет: Алгебра, автор: rinataidrisova