Помогите с Геометрией!!
Ответы
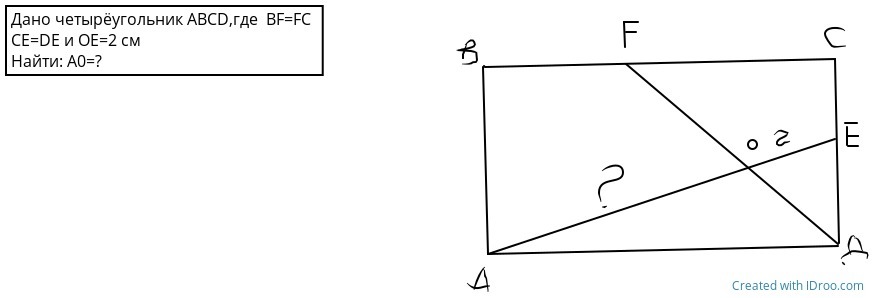
Помогите с Геометрией!!
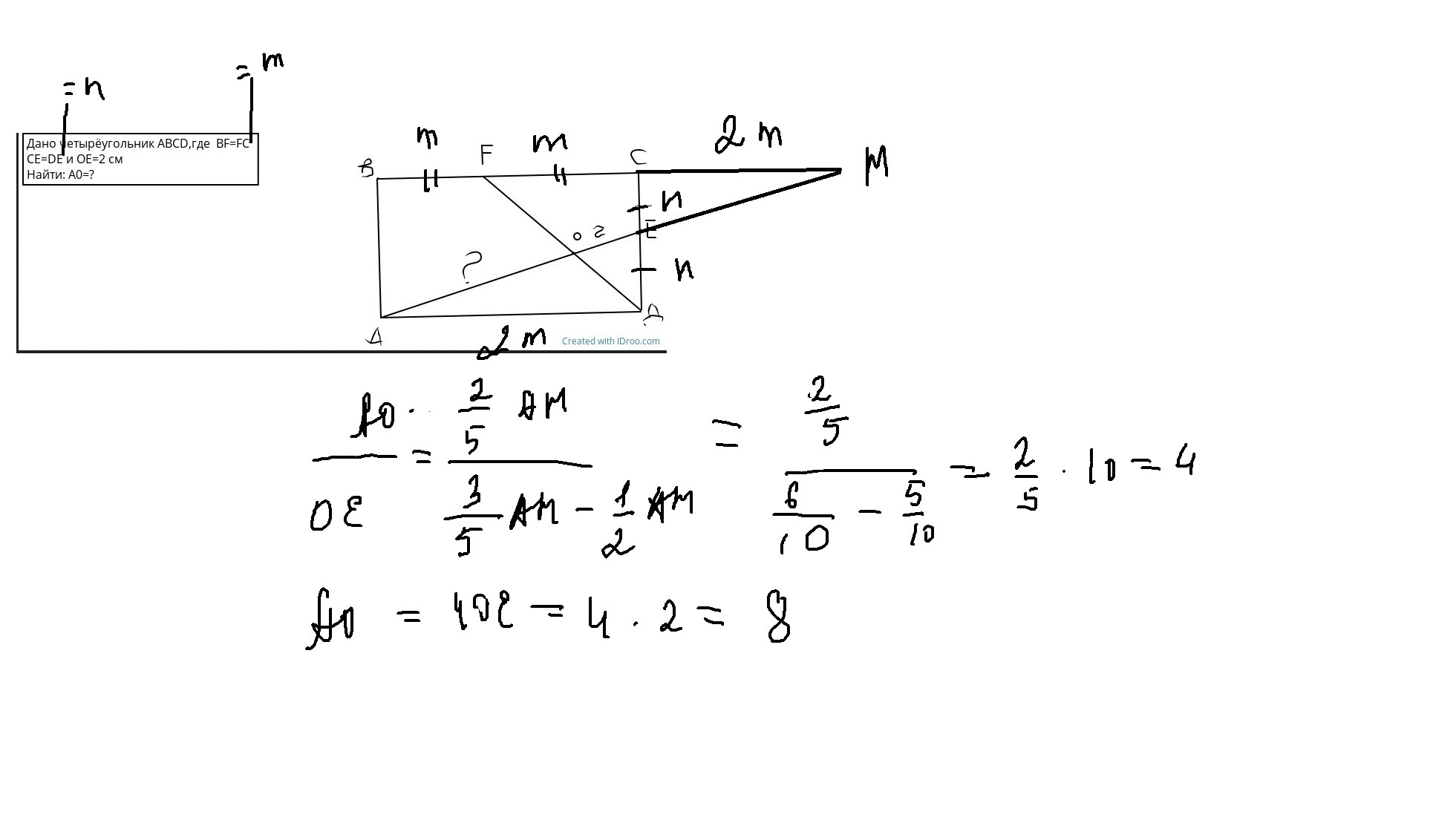
Как дополнительно нам пояснил автор задачи, ABCD - прямоугольник. Однако по зрелому размышлению я пришел к мысли, что задачу можно сделать для более широкого класса четырехугольников - параллелограммов.
Итак, пусть ABCD - параллелограмм. Продолжим FD до пересечения с продолжением AB в точке G. Легко заметить, что треугольники AGO и EDO подобия с коэффициентом подобия 4. В самом деле, углы при вершинах O в них равны как вертикальные, углы A и E - как внутренние накрест лежащие при пересечении параллельных прямых AB и DC прямой AE. Коэффициент подобия найден так: BF - это половина BC=AD и BF параллельно AD, поэтому BF - средняя линия треугольника AGD. А тогда AG=2AB=4DE. Остается написать отношение соответственных сторон AO и EO,
Ответ: 8