Предмет: Алгебра,
автор: kumarca
решите систему уравнений:
х^2+у^2=65
ху=8
Ответы
Автор ответа:
11
Выразим x через y:

Подставляем в первое уравнение вместо x 8/y:

Решаем уравнение:


ОДЗ: у≠0
y⁴-65y²+64
Пусть у²=t
t²-65t+64=0
t¹=1
t²=64
Так как у²=t
Подставляем и находим y:
y=±1; y=±8
Теперь пожсиавляем у в x=8/y
Получаем : x=±8 и х=±1
Ответ: x1,2=±8 y1,2=±1, x3,4=±1 y3,4=±8
Подставляем в первое уравнение вместо x 8/y:
Решаем уравнение:
ОДЗ: у≠0
y⁴-65y²+64
Пусть у²=t
t²-65t+64=0
t¹=1
t²=64
Так как у²=t
Подставляем и находим y:
y=±1; y=±8
Теперь пожсиавляем у в x=8/y
Получаем : x=±8 и х=±1
Ответ: x1,2=±8 y1,2=±1, x3,4=±1 y3,4=±8
maksim8716:
В ответе 1,2 и 3,4 - это индексы и там, где t¹ и t² ¹и² тоже индексы, их снизу писать
помогиии мне тожеее
алебра 14б
1-2 мин назад
приведи многочлен....
Автор ответа:
26
Решение в скане.....
Приложения:
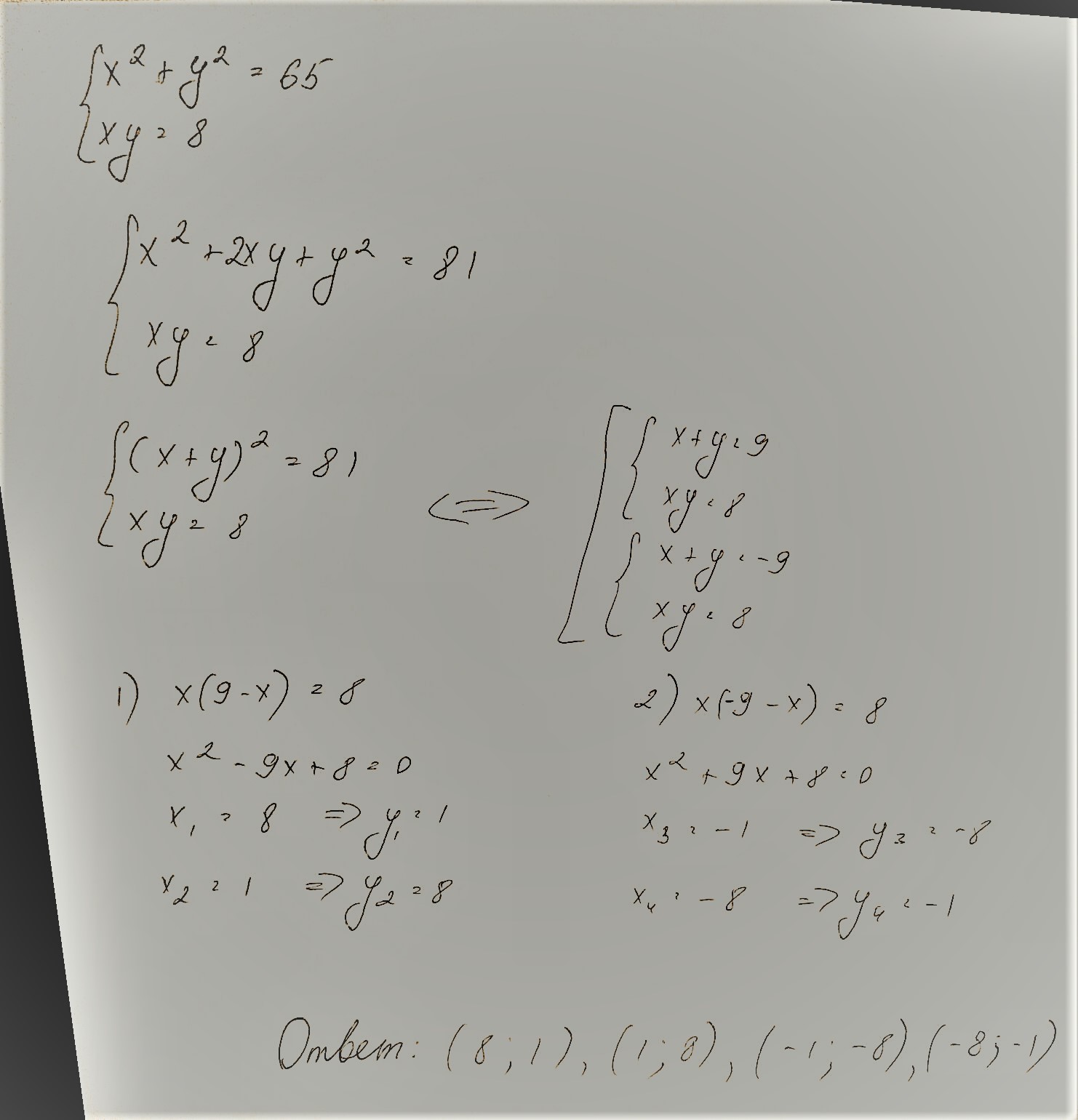
Похожие вопросы
Предмет: Физика,
автор: aslandusembinazamat
Предмет: Математика,
автор: nloseva1505
Предмет: Английский язык,
автор: popova221257
Предмет: Математика,
автор: Alm225
Предмет: Алгебра,
автор: noname1442