Предмет: Геометрия,
автор: Tamerlan3005
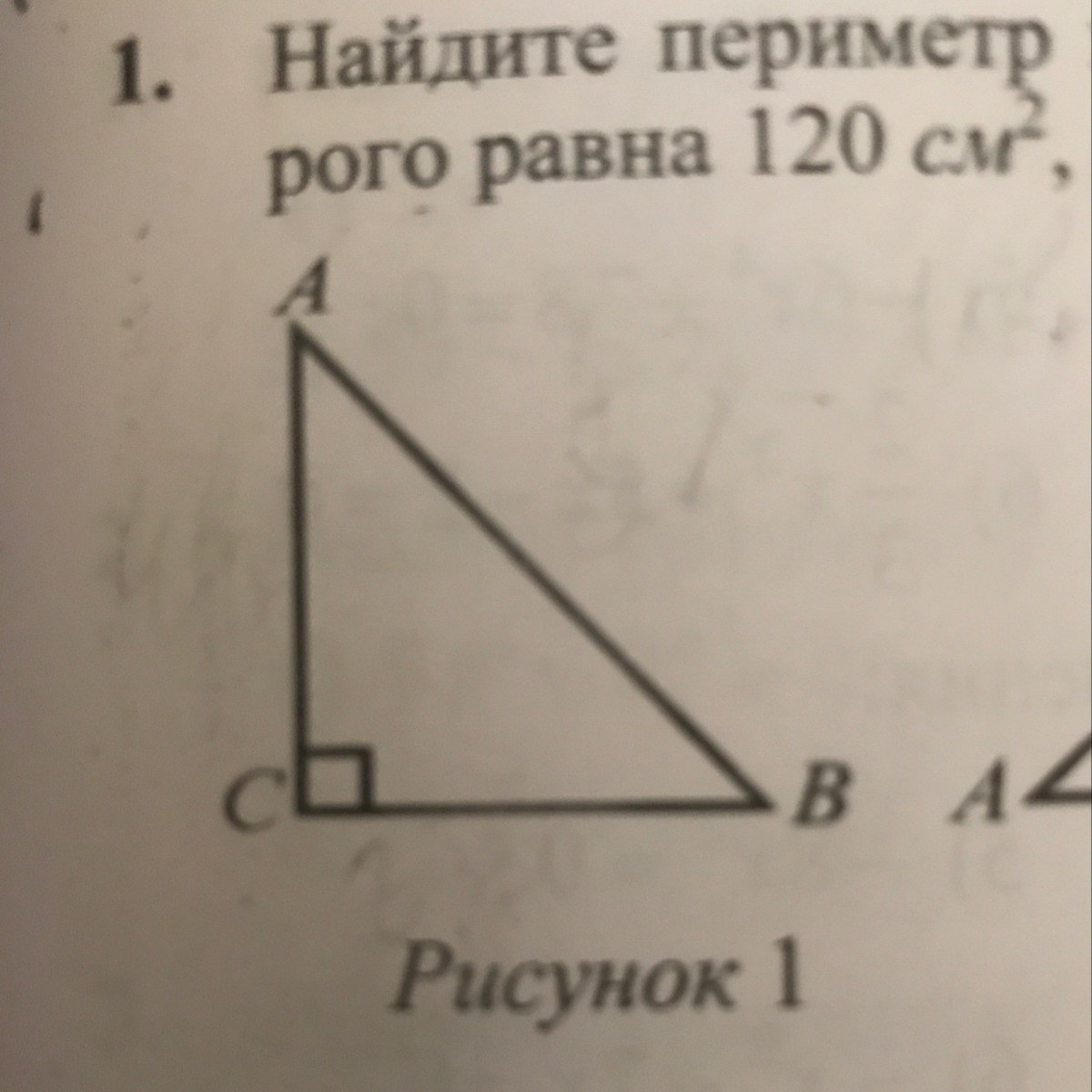
Найдите периметр прямоугольного треугольника, отношение катетов которых равно 4:3, а площадь 216см2
Приложения:
Ответы
Автор ответа:
6
1) напишем это отношение как 3х и 4х чтобы найти гипотенузу используем теорему пифагора

катеты равны 3х и 4х а гипотенуза 5x
2) находим площадь по формуле герона


Фото с обширным решением это обьеснение как найти х
а фото с маленким решением это уже мы находим периметр
катеты равны 3х и 4х а гипотенуза 5x
2) находим площадь по формуле герона
Фото с обширным решением это обьеснение как найти х
а фото с маленким решением это уже мы находим периметр
Приложения:
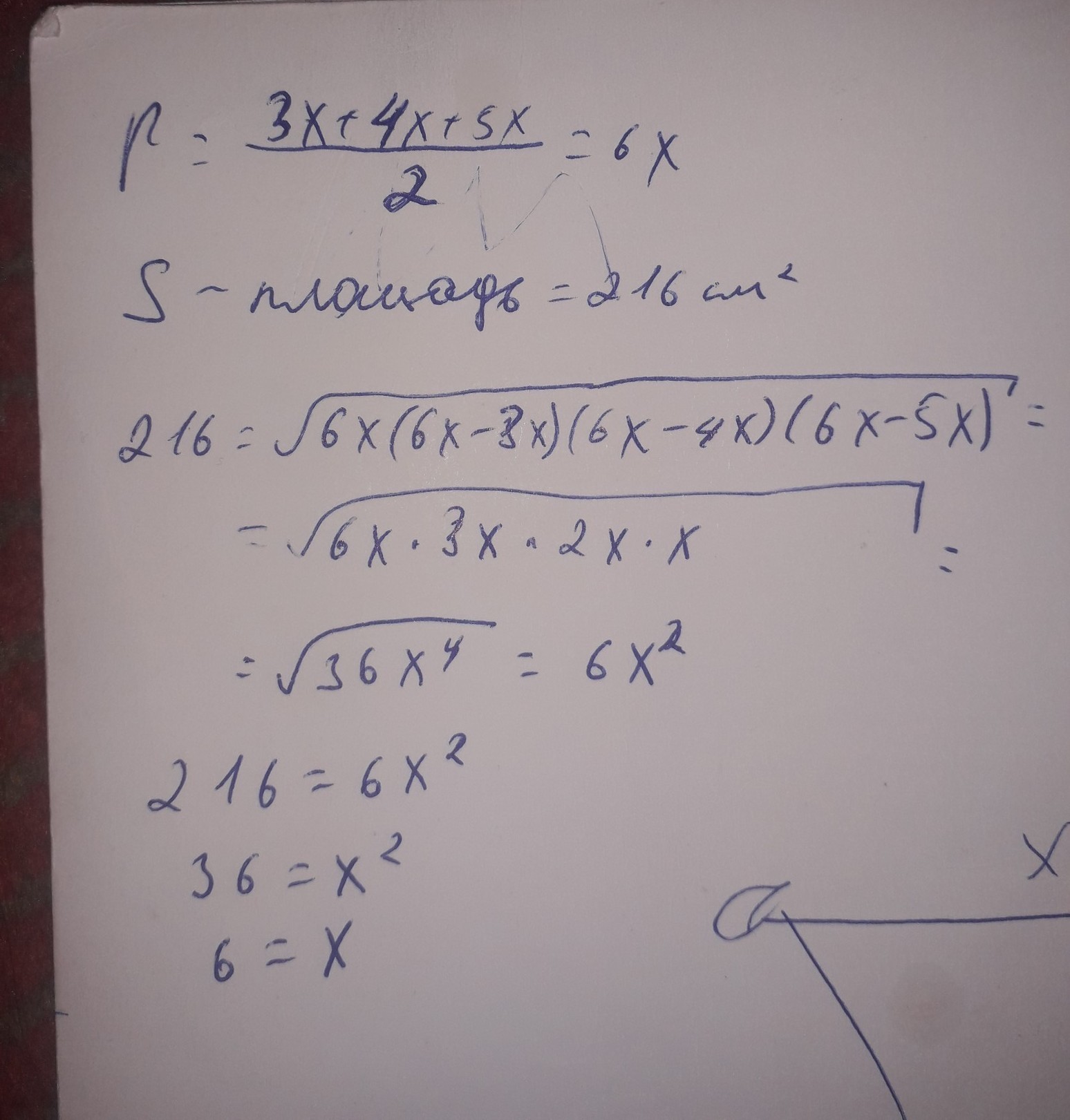

Автор ответа:
6
Ответ:
72 см.
Пошаговое объяснение:
Пусть x - одна часть, тогда AC = 4x, a CB = 3x. Получим уравнение:
(4x * 3x)/2 = 216 (Формула площади (S) прямоугольного треугольника равна половине произведения его катетов)
12x²/2 = 216
6x² = 216
x² = 216/6
x² = 36
x = √36
x = 6
AC = 4 * 6 = 24 см;
CB = 3 * 6 = 18 см.
По теореме Пифагора найдем гипотенузу:
AB² = AC² + CB²
AB² = 24² + 18²
AB² = 576 + 324
AB² = 900
AB = √900
AB = 30
P(ABC) = AC + CB + AB
P(ABC) = 24 + 18 + 30 = 72 см.
elbrusxudaverdp8qf4e:
ты допустил ошибку. Твоя формула правильная но ты умножил 3х и 4х неправильно
должно было это сделать не 12х, а 12х^2
Похожие вопросы
Предмет: Литература,
автор: serddars200831syr
Предмет: Литература,
автор: Аноним
Предмет: Русский язык,
автор: mfwdt029
Предмет: Математика,
автор: asmar2001
Предмет: Математика,
автор: NastyaSpace51