Предмет: Математика,
автор: yanuskasomer
Вычислить производную четвёртого порядка
Приложения:
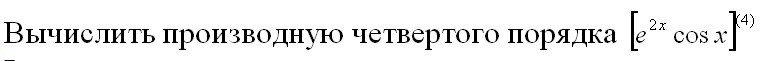
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y'=2*e^(2x)*cosx-e^(2x)*sinx=e^(2x)*(2cosx-sinx)
y"=2*e^(2x)*(2cosx-sinx)-e^(2x)*(2sinx+cosx)=e^(2x)*(4cosx-2sinx-2sinx-cosx)=e^(2x)*(3cosx-4sinx)
y'"=2*e^(2x)*(3cosx-4sinx)-e^(2x)*(3sinx+4cosx)=e^(2x)*(6cosx-8sinx-3sinx-4cosx)=e^(2x)*(2cosx-11sinx)
y""=2*e^(2x)*(2cosx-11sinx)-e^(2x)*(2sinx+11cosx)=e^(2x)*(4cosx-22sinx-2sinx-11cosx)=e^(2x)*(-7cosx-24sinx)
Похожие вопросы
Предмет: Другие предметы,
автор: myskalkurmanbekova4
Предмет: Математика,
автор: superdgoyt23
Предмет: География,
автор: explosive04
Предмет: Геометрия,
автор: tanyaivanovat
Предмет: Алгебра,
автор: katyaveretelni