Question

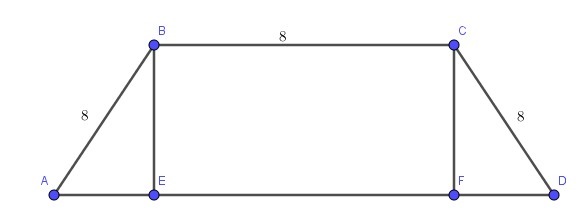
найдите наибольшую площадь трапеции, три стороны которой равны 8 см

Answer 1

Основание AD не может быть равен 8, так что AB=BC=CD=8 см.

Обозначим AD=x, тогда $AE=FD=\dfrac{AD-BC}{2}=\dfrac{x-8}{2}$

Из прямоугольного треугольника CFD, по теореме Пифагора:

$CF=\sqrt{64-\dfrac{(x-8)^2}{4}}=\dfrac{1}{2}\sqrt{192+16x-x^2}$

Рассмотрим функцию: $S(x)=\dfrac{x+8}{2}\cdot\dfrac{1}{2}\sqrt{192+16x-x^2}=\dfrac{x+8}{4}\sqrt{192+16x-x^2}$

Производная функции:

$S'(x)=\dfrac{1}{4}\sqrt{192+16x-x^2}+\dfrac{x+8}{4}\cdot\dfrac{(16-2x)}{2\sqrt{192+16x-x^2}}=\\ \\ =\dfrac{192+16x-x^2+64-x^2}{4\sqrt{192+16x-x^2}}=\dfrac{256+16x-2x^2}{4\sqrt{192+16x-x^2}}=0~~\Leftrightarrow~~ x=16$

$192+16x-x^2>0~~~\Leftrightarrow~~~ x \in (-8;24)$

(0)___+___(16)__-___(24)

Производная функции в точке х=16 меняет знак с (+) на (-), следовательно, х=16 - точка максимума.

$S(16)=\dfrac{16+8}{4}\sqrt{192+16\cdot16-16^2}=6\sqrt{192}=48\sqrt{3}$ см²

Ответ: 48√3 см²

Answer 2

Трапеция равнобокая .

Пусть углы А и D как на рисунке х.

Тогда высота трапеции 8*sin(x)

А площадь

S = 8* 8 * sin(x) + 2 * 8* cos(x) * 8 * sin (x) / 2 = 64 * ( sin(x) + sin(2x)/2 )

S' = 64 * ( cos(x)+cos(2x))= 64 * (2cos^2(x)+cos(x)-1)

S'=0

2соs^2(x)+cos(x)-1=0

cos(x)= -1 - это минимум

cos(x)=1/2 - это максимум

Синус х при этом равен √3/2

Синус 2x при этом x тоже √3/2

S max = 64 ( √3/2+ √3/4)= 48 √3 см^2