Question

ПОМОГИТЕ СРОЧНО РЕШИТЬ С РИСУНКОМ И ОБЪЯСНЕНИЕМ , ДАЮ 40 БАЛЛОВ

Answer 1

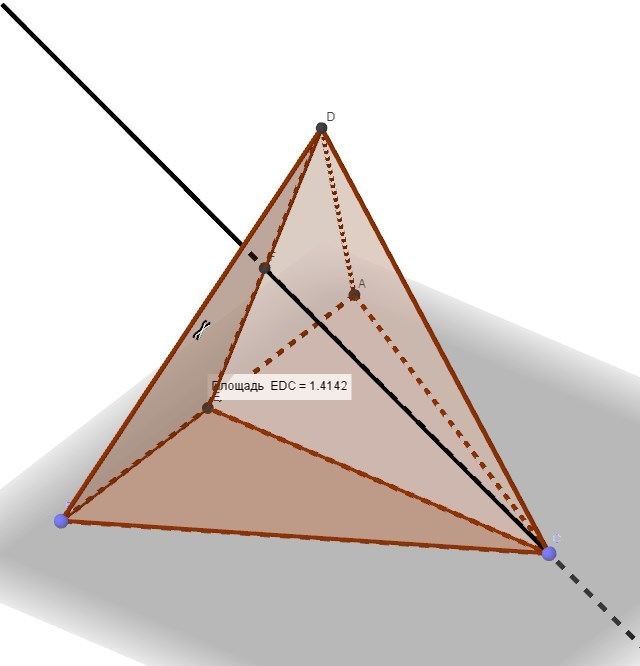
Добрый день! Дано: DABC - тетраэдр M - середина AB  АB = a.  Найти: S(MDC) = ?

Решение:

Построим сечение MDC.

1) Точки M и C принадлежат плоскости основания (ABC) => их можно соединить (по одной из аксиом стереометрии)

2) Точки М и D принадлежат плоскости ABD => их можно соединить.

Получаем искомое сечение MDC

Так как дан тетраэдр, то ABD и ABC - правильные треугольники => DM и MC - медианы, высоты, биссектрисы, а также DM = MC  = $\frac{a\sqrt{3} }{2}$ где a - сторона

DC - ребро тетраэдра => DC = AB = a

Так как треугольник DMC - равнобедренный, то высота, проведённая из точки M к прямой DC, является медианой и пересекает DC в точке F

По теореме Пифагора для треугольника FMC получим, что

FM = $\frac{a}{\sqrt{2}}$

Таким образом, S(MDC) = 1/2 * FM * DC  = $\frac{a^{2} \sqrt{2} }{4}$

В прикреплённом файле, рисунок тетраэдра со стороной 2, то есть a = 2

=> Площадь сечения = $\sqrt{2}$