Предмет: Алгебра,
автор: JIuC2003
помогите пж! как это решать? пример под буквой а)
Приложения:
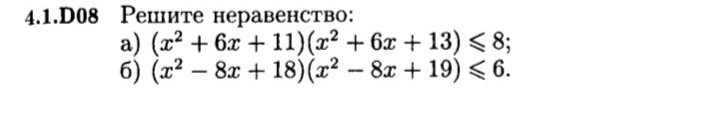
Ответы
Автор ответа:
1
(вторую скобку отбросили в силу ее положительности, ведь старший коэффициент положителен, а дискриминант отрицательный). Поскольку квадрат числа не может быть отрицательным, последнее неравенство равносильно уравнению
Ответ:
Автор ответа:
2
Похожие вопросы
Предмет: Биология,
автор: zhansayaaskhatkyzy20
Предмет: Психология,
автор: tgejger
Предмет: Другие предметы,
автор: eibelsaifer12345
Предмет: Биология,
автор: danilmaksimov3
Предмет: Биология,
автор: Araneae