Предмет: Алгебра,
автор: JIuC2003
помогите пж! как это решить? пример по буквой а)
Приложения:
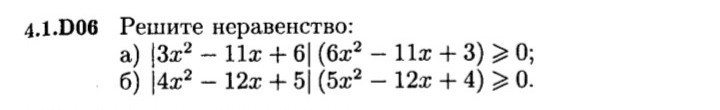
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: citrus900
Предмет: Математика,
автор: MaGmAYTT
Предмет: Математика,
автор: tuleshevd
Предмет: Алгебра,
автор: anasia30032003