Предмет: Информатика, автор: kookbak

Отметьте штриховкой на координатной плоскости область, в
которой и только в которой данное логическое выражение имеет значе-
ние true. Если граница входит в область, то обозначать её сплошной
линией, если нет, то – штриховой.
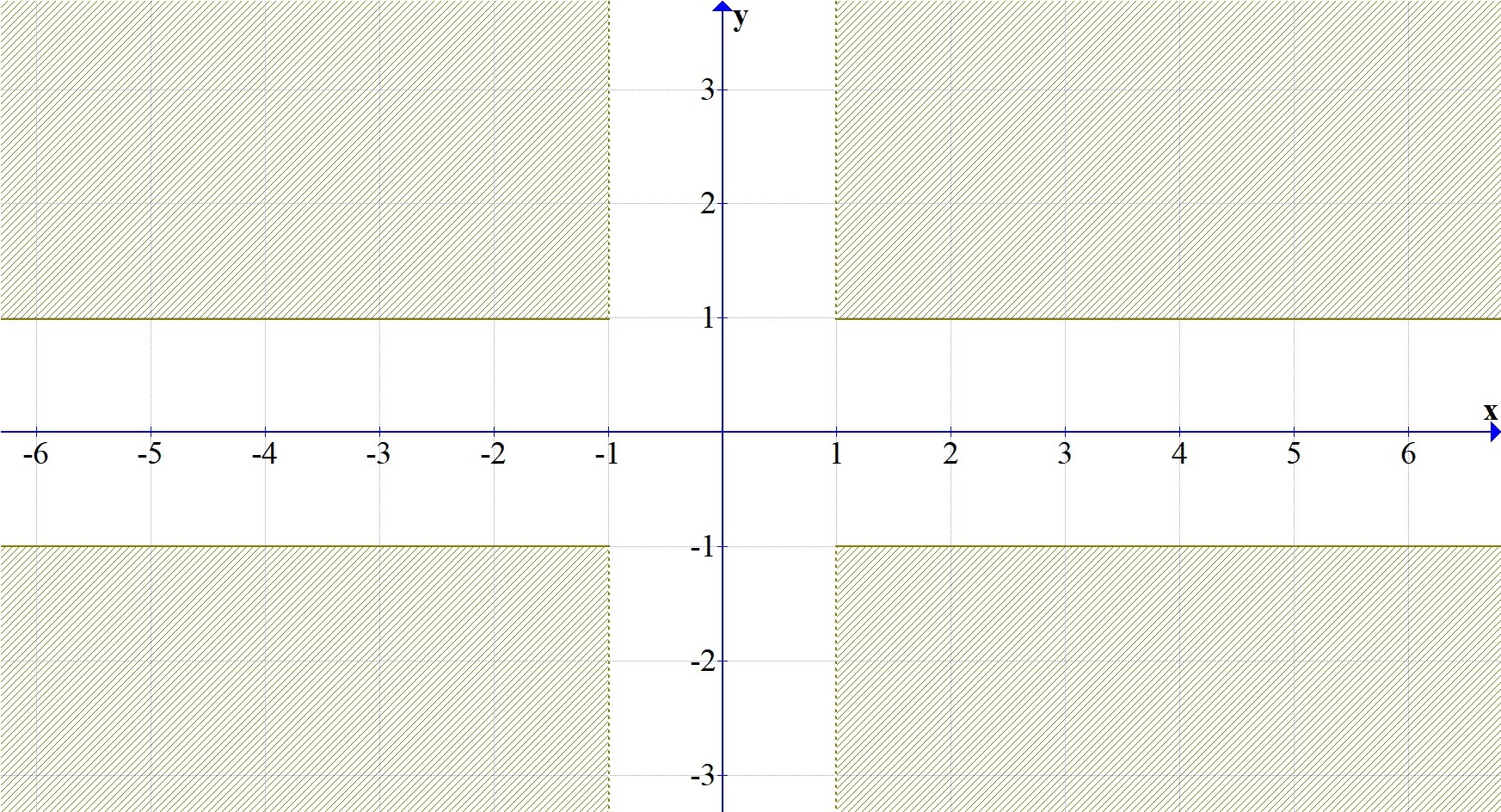
а) (sqr(x)>1)and(sqr(y)>=1)
б) (sqr(x)+sqr(y)>9)=(abs(y)+abs(x)<=2)

csharp: Попробую.

kookbak: У вас получилось?

csharp: Да, я первое сделал, а потом посмотрел на второе.. В общем, с модулями у меня проблема, рисовать их не очень-то и хотелось. Но в целом всё просто: sqr - это возведение в квадрат. В первом получается, я так понял, четыре квадрата. Во втором получается окружность вместе с ромбом.

kookbak: А какие области заштрихованы? Мне без рисунка не очень понятно.

csharp: В первом задании у Вас неравенство x^2 > 1, переносим вправо: x^2 - 1 > 0, раскладываем по формуле разность квадратов: (x - 1)(x + 1) > 0. Отмечаете эти значения на координатной плоскости. Берётесь за другое неравенство: y^2 >= 1. Также переносите влево единицу: y^2 - 1 >= 0 и также раскладываете: (y - 1)(y + 1) >= 0. Отмечаете.

kookbak: А под буквой б?

csharp: Не знаю, что подразумевается под собой равенство этих двух неравенств.

kookbak: А линии там какие штриховкой или сплошные?

csharp: В неравенстве x^2 > 1 штрихованные.

kookbak: А y^2>=1?

Ответы

Автор ответа: Ziorar

Области показаны на приложенных скриншотах.

В примере б) левое и правое неравенство (когда они истинные) дают не пересекающиеся области на плоскости. Левое неравенство- всё, что вне окружности радиусом 3, а правое- всё, что внутри ромба, целиком находящегося внутри вышеупомянутой окружности. Поэтому, всё выражение будет истинным, только если оба неравенства будут ложными (дадут результат false).

Приложения: