Здравствуйте, помогите пожалуйста. Решить методом Крамера, Матричным, Гаусса или одним из них, заранее спасибо.
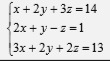
Ответы
Используем метод Гаусса. Умножив второе уравнение на 3, а третье на 2, получим систему:
x+2*y+3*z=14
6*x+3*y-3*z=3
6*x+4*y+4*z=26
Теперь заменим третье уравнение системы разностью третьего и второго. Получим систему:
x+2*y+3*z=14
6*x+3*y-3*z=3
y+7*z=23
Умножим теперь первое уравнение на 6 и заменим после этого второе уравнение разностью первого и второго. Мы получим систему:
6*x+12*y+18*z=84
9*y+21*z=81
y+7*z=23
Умножим теперь третье уравнение на 9 и заменим третье уравнение разностью третьего и второго. Получим систему:
6*x+12*y+18*z=84
9*y+21*z=81
42*z=126
Из третьего уравнения находим z=126/42=3. На этом прямой ход метода Гаусса закончен и начинается его обратный ход.
Подставляя z=3 во второе уравнение, находим y=2. Подставляя z=3 и y=2 в первое уравнение, находим x=1. Подставляя значения x=1,y=2 и z=3 в исходную систему, убеждаемся, что этот набор действительно является единственным решением системы.
Ответ: x=1, y=2, z=3.