Решите, используя формулу полной вероятности. 1.Трое рабочих за смену изготовили 60 деталей. Производительность рабочих относится как 1:2:3. Первый рабочий изготавливает в среднем 95% годных деталей, второй – 85% и третий – 90%. Найти вероятность того, что наудачу взятая из числа изготовленных за смену деталь низкого качества.
Ответы
Ответ: Вероятность брака - 13/120 ≈ 0,1083 ≈ 10,8%.
Даны такие "неудобные" числа, что даже трудно выбрать как вычислять - точно, но в натуральных дробях или приблизительно - в десятичных.
НАЙТИ: Вероятность БРАКА.
Пошаговое объяснение:
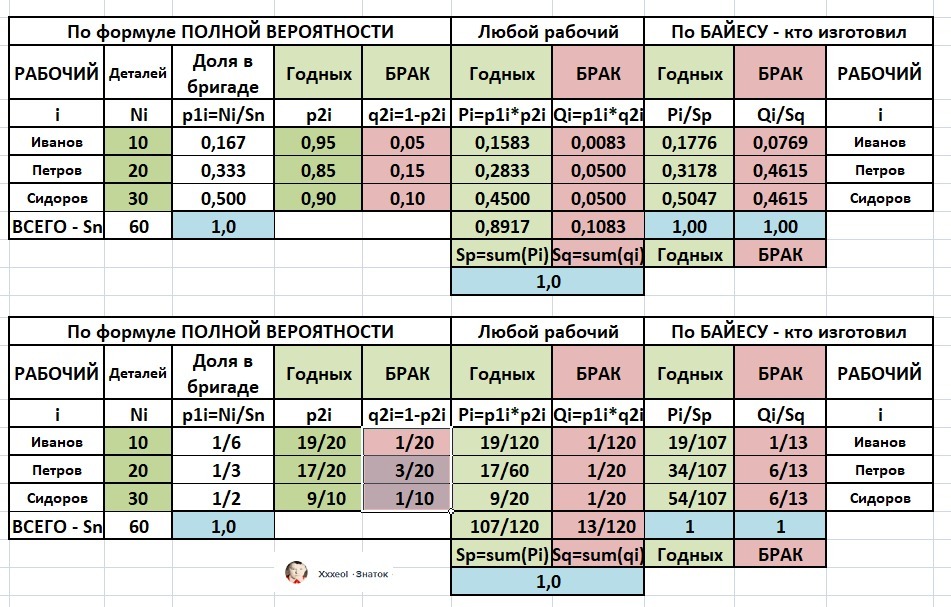
Расчет сведен в таблицу и даже в двух вариантах. Таблица в приложении.
Для определённости дадим рабочим традиционные русские фамилии.
Мой ответ - "Ответ Замятина - НЕ НУЖНОЕ - не использовать - дано для общего развития."
Событие по задаче - случайная деталь и будет браком состоит из двух независимых.
Вероятность выбрать случайную деталь из 60 штук находим разделив в отношении 1:2:3 и получаем:
Р11 = 1/6, Р12=1/3 и Р13= 1/2. - вероятности выбрать случайную деталь из 60 штук. Проверили - сумма равна 1 (доля в бригаде).
Теперь находим вероятность БРАКА у каждого рабочего по формуле: Q= 1 - P.
q21 = 1 - p21 = 1 - 0.95 = 0.05 = 1/20 - вероятность брака у Иванова.
Аналогично: q22 = 0,15 = 3/20, q32 = 0,1 = 1/10 - у других рабочих.
И теперь собственно решение задачи: случайная задача будет браком состоит из трёх событий: Иванов И брак ИЛИ Петров И брак ИЛИ Сидоров И брак. Пишем формулу:
Q(А) = p11*q21 + p21*q22 + p31*q23 = 1/120 + 1/20 + 1/20 = 13/120 - вероятность бракованной детали.
Понятно, что вероятность годной детали будет: P(A) = 1 - Q(A) = 107/120 - ответ точный или то же но в десятичных дробях - 0,1083 - брак и 0,8917 - годные.
А далее по формуле Байеса находим, что этот брак сделал НЕ ИВАНОВ.