Question

Здраствуйте, извесно что в квадратичной функции ax^2+bx+c
если x — больше 0 то то парабола с ветвями вверх, если менше с ветвями вниз... А какие свойства у b и c...

Answer 1

а більший 0 бо парабола вітками вниз.
с=0 бо графік функції перетинає центр координат
б більший за 0. координата х вершини більша за нуль і має формулу -b/2a. тобто щоб бути додатньою б має бути більшим за 0.

Answer 2

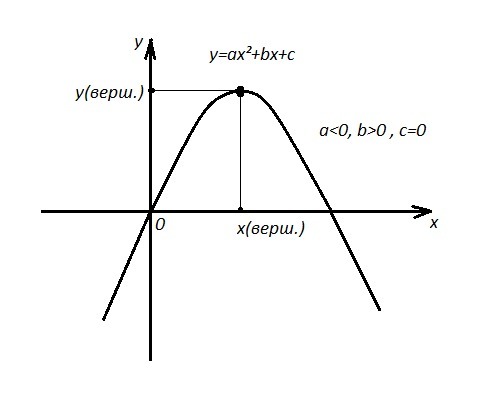
ЗНО 2010.     y=ax²+bx+c

1)  По графику видно, что ветви параболы направлены вниз, поэтому  a<0.

2)  Ордината точки пересечения параболы с осью ОУ находится из равенства у=у(0), то есть у(0)=а·0²+b·0+c=c. Отсюда имеем координаты точки пересечения параболы и оси ОУ: (0,с).

Так как на рисунке видно, что точка пересечения имеет координаты (0,0), то с=0.

В общем случае ордината точки пересечения параболы и оси ОУ - это значение "с". Если c>0 , то точка пересечения - выше оси ОХ, а если c<0, то точка пересечения - ниже оси ОХ.

3) Абсцисса вершины параболы находится по формуле х(верш)= -b/2a . Так как по рисунку видно, что х(верш)>0 , то  $\frac{-b}{2a}>0$  . Учтём, что  а<0 , тогда дробь  $\frac{-b}{2a}$  будет положительной при  $b>0$  .

Коэффициент  "b"  в общем случае отвечает за то , где находится вершина параболы. В каждом конкретном случае надо определять знак  "b"  в зависимости от знака коэффициента  "а" .

Ответ:  a<0 , b>0 , c=0  (ответ под буквой Д) .