Предмет: Алгебра,
автор: Jina9845
Ставлю 30 баллов!!! Распишите подробно на листочке!!
Приложения:
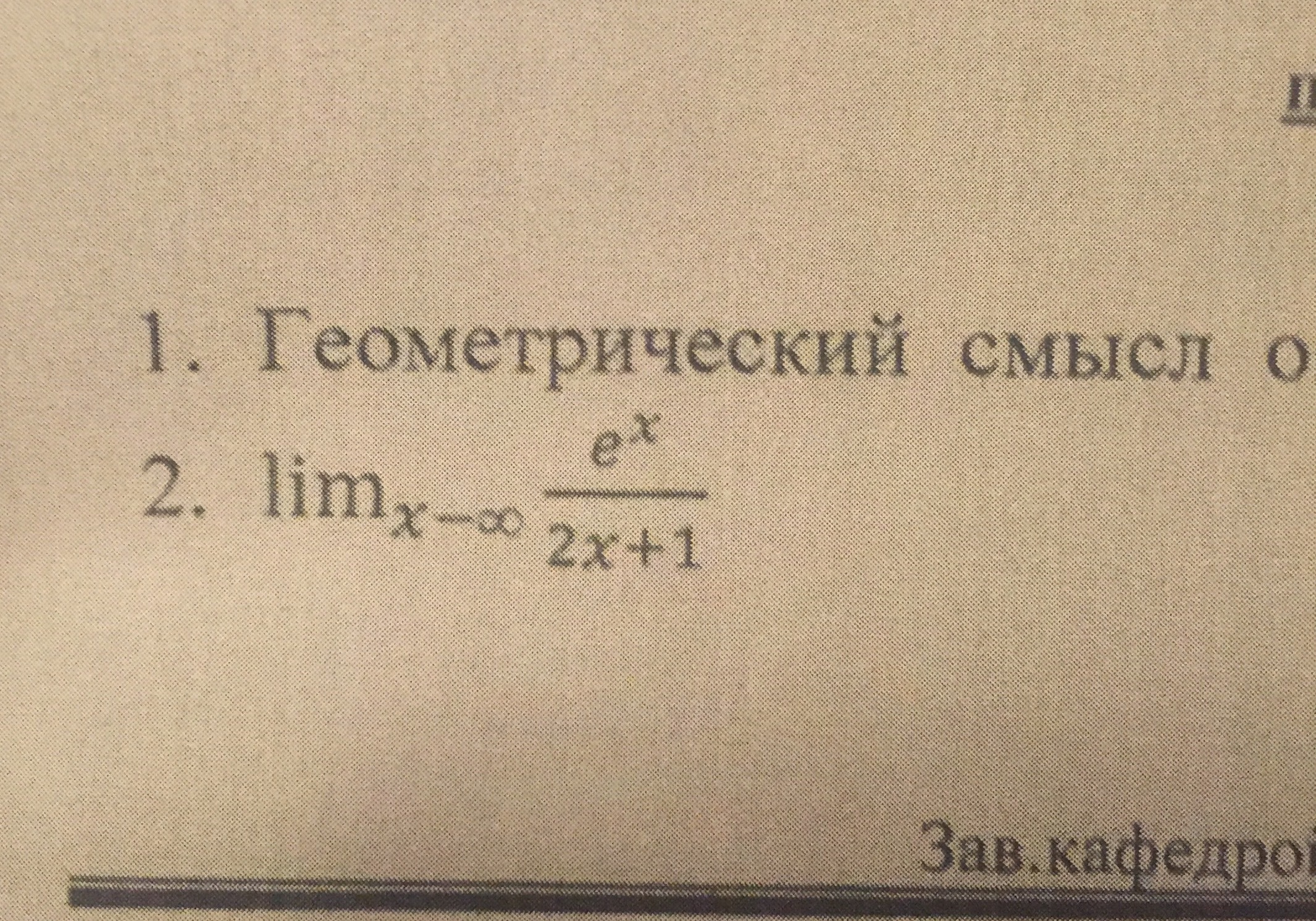
Ответы
Автор ответа:
1
Подробное решение на картинке.
Приложения:
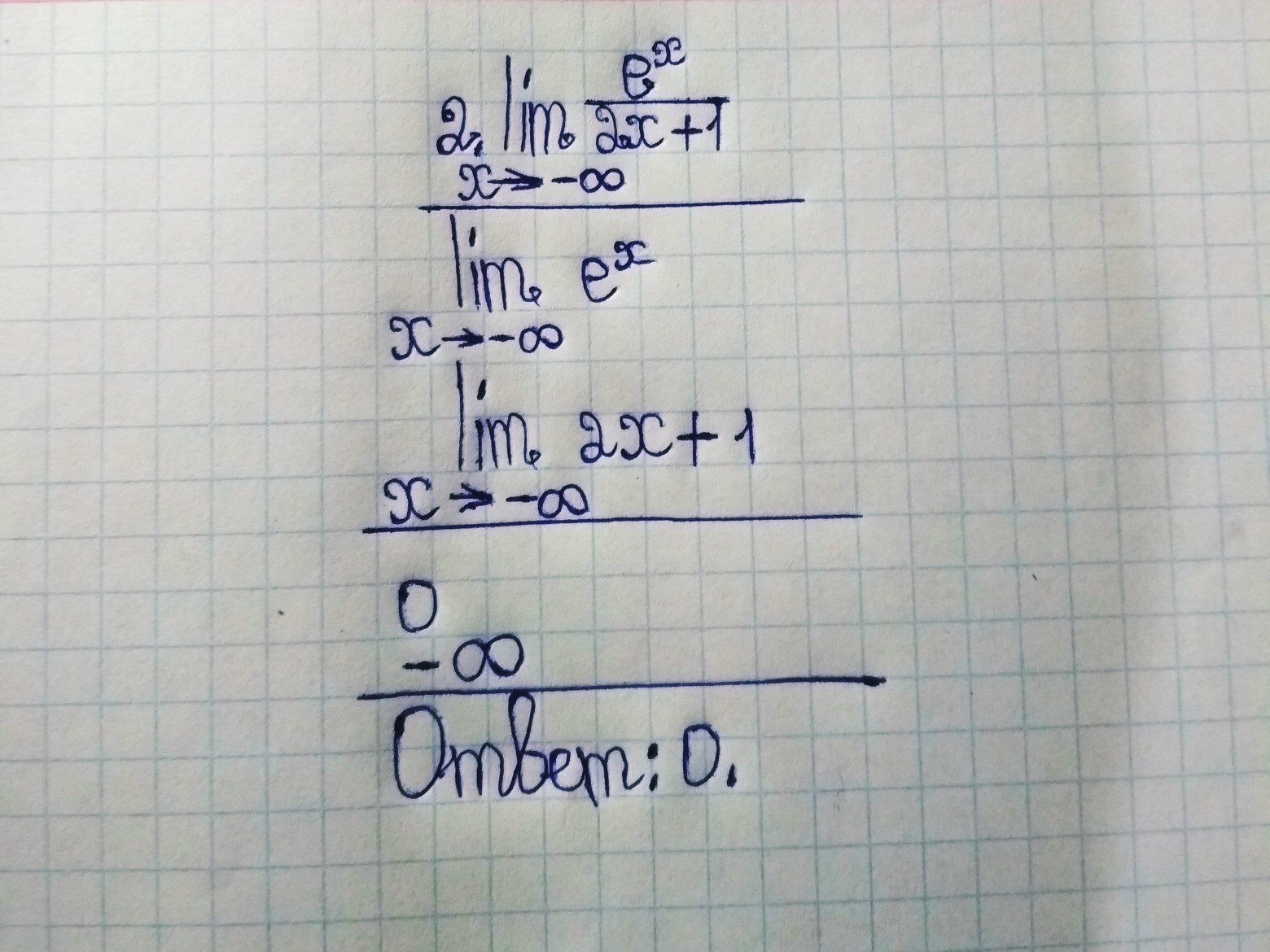
Автор ответа:
1
Применим правило Лопиталя:
Вычислим пределы числителя и знаменателя:
Поскольку выражение определено как
, следовательно, предел
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: marjonsardor
Предмет: Литература,
автор: kv22vedmeckiig
Предмет: История,
автор: sambar2779
Предмет: Математика,
автор: Vredina06
Предмет: Литература,
автор: Roza2057