Question

18 баллов !!! Решите задачу 2.6

Answer 1

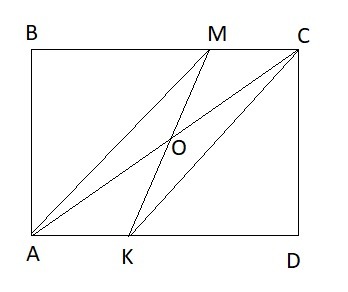
∠AOK = ∠MOC (вертикальные)

∠MCO = ∠KAO (накрест лежащие)

AO = OC (O - середина AC) ⇒ ΔAOK = ΔMOC (по стороне и двум прилегающим углам

Отсюда MC = AK и MC ║AK ⇒ AMCK - параллелограмм

Найдем высоту параллелограмма CD по теореме Пифагора из прямоугольного ΔACD:

$CD=\sqrt{AC^2-AD^2}=\sqrt{AC^2-(AK+KD)^2}=\sqrt{15^2-12^2}=9$

Теперь найдем площадь параллелограмма AMCK:

$S_{AMCK}=AK*CD=4*9=36$