Предмет: Математика,
автор: jixenozadu
Помогите решить задание по матетмаики ЕГЭ
Приложения:
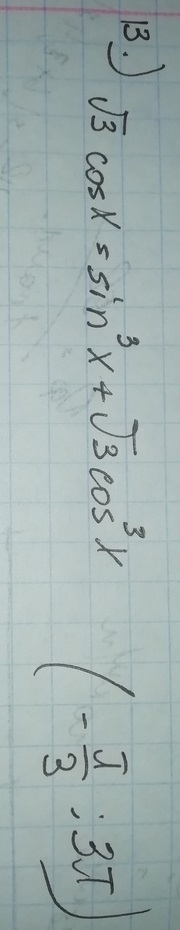
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
С учетом заданного интервала
С учетом заданного интервала
Автор ответа:
1
а) √3•сosx = sin³x + √3•cos³x
√3•cosx - √3•cos³x - sin³x = 0
√3•cosx•( 1 - cos²x ) - sin³x = 0
√3•cosx•sin²x - sin³x = 0
sin²x • ( √3•cosx - sinx ) = 0
1) sin²x = 0 ⇒ sinx = 0 ⇒ x = пn , n ∈ Z
2) √3•cosx - sinx = 0 ; делим обе части данного уравнения sinx ≠ 0
√3•cosx/sinx - sinx/sinx = 0
√3•ctgx - 1 = 0
ctgx = 1/√3 = √3/3
x = п/3 + пk , k ∈ Z
б) С помощью тригонометрической окружности отберём корни, принадлежащие промежутку ( - п/3 ; 3п ):
х₁ = 0 при n = 0 ***** х₂ = п/3 при k = 0
х₃ = п при n = 1 ***** x₄ = п + п/3 = 4п/3 при k = 1
x₅ = 2п при n = 2 ***** x₆ = 2п + п/3 = 7п/3 при k = 2
ОТВЕТ: а) пn, n ∈ Z ; п/3 + пk, k ∈ Z ; б) 0 ; п/3 ; п ; 4п/3 ; 2п ; 7п/3
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: dudchenkostas111
Предмет: География,
автор: kv22vedmeckiig
Предмет: Алгебра,
автор: tosya01
Предмет: Математика,
автор: TomaSwm