Предмет: Математика,
автор: romantikaalena
Найти области определения функций одной переменной! 20 баллов!
Приложения:
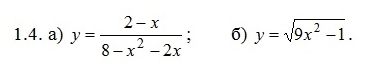
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
а) функция у = (2 - х)/(8 - х² - 2х)
Знаменатель функции не должен быть равен нулю
-х² - 2х + 8 = 0
D = 4 + 32 = 36 √D = 6
x1 = (2 - 6)/(-2) =2
x2 = (2 + 6)/(-2) = -4
Итак, х ≠ -4 и х ≠ 2
Запишем ответ в интервалах:
область определения D(y) = (-∞; -4) U (-4; 2) U (2; +∞)
б) у = √(9х² - 1)
Подкоренное выражение не должно быть отрицательным
9х² - 1 ≥ 0
х1 ≤ -1/3 и х2 ≥ 1/3
В интервалах. область определения функции равна
D(y) = (-∞; -1/3] U [1/3; +∞)
antonovm:
ОЙ , извините Лена , у вас все верно , нарушений нет
Похожие вопросы
Предмет: Русский язык,
автор: enotiktrader322
Предмет: Математика,
автор: gkgxkgiiixgkgxlg
Предмет: Қазақ тiлi,
автор: deydarochka228
Предмет: Математика,
автор: manzulova70
Предмет: Литература,
автор: маша7101