Предмет: Геометрия,
автор: nastya77943
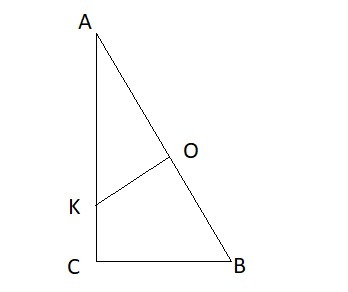
В прямоугольном треугольнике АВС с катетами ВС=8, АС=10 через центр О описанной около треугольника окружности проведена прямая, перпендикулярная его гипотенузе и пересекающая больший катет в точке К. Найдите длину отрезка АК.
Ответы
Автор ответа:
2
По теореме Пифагора
Т.к. центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы, то
ΔABC ≈ ΔAOK (по трем углам) ⇒
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: danan8584
Предмет: Математика,
автор: arinamyasnikova1999
Предмет: Математика,
автор: digry42
Предмет: Геометрия,
автор: antropovad12
Предмет: Биология,
автор: МээээриПоппинс