Question

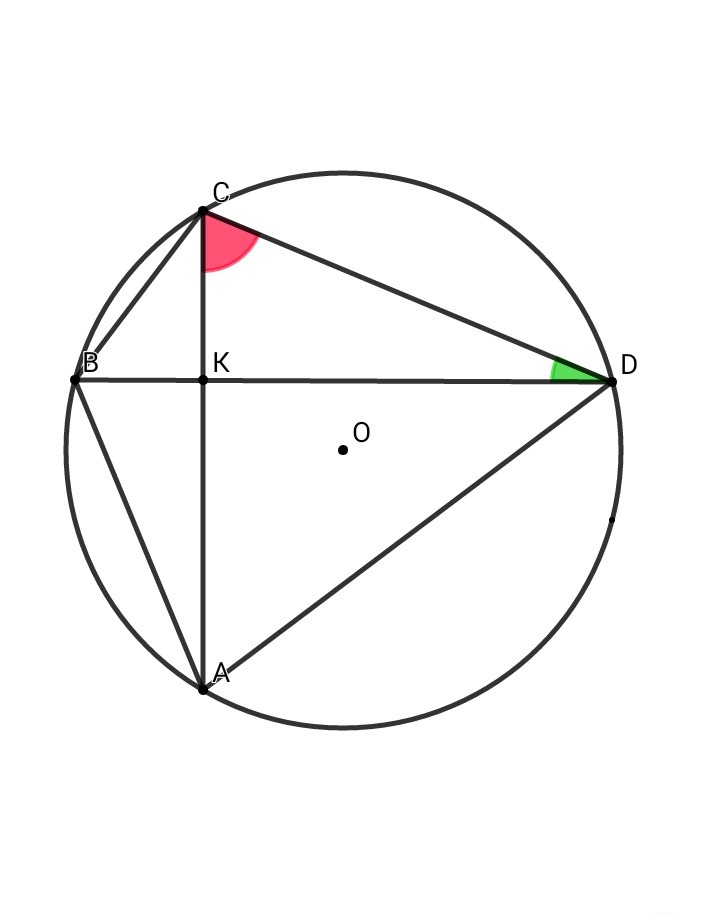
в круге радиуса R проведены две пересекающиеся под прямым углом хорды. Найти а) сумму квадратов четырех отрезков этих хорд, на которые последние делятся точкой пересечения
Подскажите хотябы каким методом решать

Answer 1

Еще  одно решение ( другое )

Answer 2

▪ Теорема Пифагора

Проведём из точки D отрезок DE, параллельный диагонали АС, тогда  ∠BDE = ∠BAE = 90° , BE - диаметр окружности  ⇒  АСDE - равнобедренная трапеция  ⇒  CD = AЕ

В ΔВАЕ по т. Пифагора: AB² + AE² = BE²  ⇒  AB² + CD² = ( BK² + AK² ) + ( CK² + KD² ) = BE² = ( 2R )² = 4R²

Значит, BK² + AK² + CK² + KD² = 4R²

или

Построим диаметр окружности ВЕ, тогда ∠ВАЕ = 90°

∠ВСА = ∠ВЕА - как вписанные углы, опирающиеся на общую дугу АВ

Из прямоугольных треугольников ВКС и ВАЕ следует, что ∠CBD = ∠ABE  ⇒  CD = AE - как хорды, стягивающие равные дуги CD и АЕ

В ΔВАЕ по т. Пифагора: AB² + AE² = BE²  ⇒  AB² + CD² = ( BK² + AK² ) + ( CK² + KD² ) = BE² = ( 2R )² = 4R²

Значит, BK² + AK² + CK² + KD² = 4R²

▪ Теорема синусов

Пусть ∠CDК = α , тогда ∠KCD = 90° - α

В ΔBCD по т. синусов:  ВС/sinα = 2R  ⇒  BC = 2R•sinα

В ΔACD по т. синусов:  AD/sin( 90° - α ) = 2R  ⇒  AD = 2R•cosα

BC² + AD² = ( 2R•sinα )² + ( 2R•cosα )² = 4R²•sin²α + 4R²•cos²α = 4R²•( sin²α + cos²α ) = 4R²

Значит, BK² + CK² + AK² + KD² = 4R²