Question

Помогите с геометрии, даю 50 баллов.
Дали на каникулы.
8 класс. Тема: Решение прямоугольных треугольников
1) Найдите катеты и второй острый угол прямоугольного треугольника, у которого гипотенуза с = 12 см и угол a = 38°. Округлите значение катетов с точностью до сотых
2) Отношение катетов прямоугольного треугольника равен 5 : 2. Найдите (с точностью до градусов) острые углы этого треугольника.
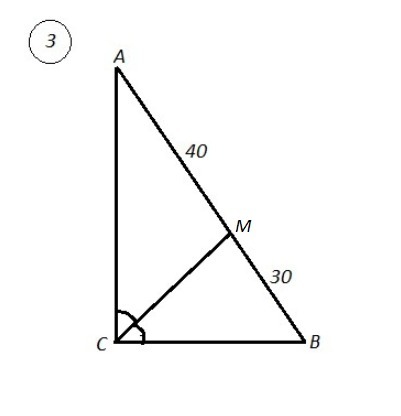
3) Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки 30 дм и 40 дм. Найдите периметр треугольника
(Не знаю, думаю рисунок не в тему↓)

Answer 1

1) Второй угол_в=52°
По т. синусов: а/sin38=12/1, a=7.39 см, в=9.46 см
2) первый_у=arctg(5/2)=68°, второй-у=22°
4) (рис) у.а=arctg(8/15)=28°, у.в=62°

Answer 2

1)  ΔАВС , ∠С=90° , ∠А=38° ,  с=АВ=12 см .

∠В=90°-38°=52°  

sin∠A=CB/АВ=CB/12  ⇒  CB=12·sin38°≈12·0,62=7,44

sin∠B=AC/AB=AC/12  ⇒  AC=12·sin52°≈12·0,79=9,48

2)  ΔАВС , ∠С=90° ,  АC/ВС=5/2  ⇒  АС=5х ,  ВС=2х  ⇒  

tg∠A=2x/5x=2/5=0,4  ⇒  ∠A=arctg0,4≈22°

tg∠B=5x/2x=5/2=2,5  ⇒  ∠B=arctg2,5≈68°   ( или  ∠В=90°-22°=68° )

3)  ΔАВС ,  ∠С=90°  ,  СМ - биссектриса ,  АМ=40 дм , ВМ=30 дм .

СМ - биссектриса  ⇒  АМ/АС=ВМ/ВС  ⇒  АМ/ВМ=АС/ВС  ,  40/30=АС/ВС  

АС/ВС=4/3  ⇒  АС=4х  ,  ВС=3х ,

АВ=√(АС²+ВС²)=√((4х)²+(3х)²)=√25х²=5х ,

АВ=АМ+ВМ=40+30=70   ⇒    5х=70  ,

х=70:5=14 (см)

АС=4х=4·14=56 (см)  ,  ВС=3·14=42 (см) ,

Периметр  Р=АС+ВС+АВ=56+42+70=168 см .