Question

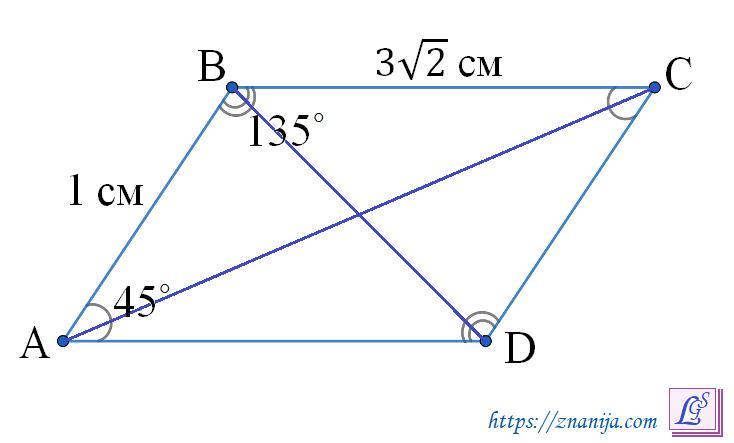
Сторони паралелограма дорівнюють3√2см і 1см, один з його кутів дорівнює 45°.Знайдіть більшу діагональ паралелограма.

Answer 1

Ответ:

Большая диагональ равна 5 см.

Пошаговое объяснение:

Дано: ABCD параллелограмм, AB = 1 см, BC = 3√2 см. Найти длину большей диагонали.

Решение.

1) Два угла, ∠A и ∠B, прилежащие одной стороне параллелограмма являются внутренними односторонними углами при параллельных прямых BC║AD и секущей AB. Их сумма равна 180°.

Найдем ∠B:

∠A + ∠B = 180°; ∠B = 180° - ∠A = 180° - 45° = 135°.

2) В параллелограмме против большего угла лежит большая диагональ, против меньшего угла лежит меньшая диагональ.

Это следует из теоремы: в треугольнике против большего угла лежит большая сторона. ΔABC и ΔABD образованы двумя равными отрезками и диагоналями параллелограмма: AB - общая сторона обоих треугольников, DC = AD как противолежащие стороны параллелограмма. Тогда AC больше, чем BD, так как ∠В = 135° в ΔABC больше, чем ∠A = 45° в ΔABD.

⇒ AC - это большая диагональ параллелограмма.

3) Найдем длину AC по теореме косинусов из ΔABC.

AC² = AB² + BC² - 2*AB*BC*CosB

$\displaystyle Cos B = Cos 135^{o} = Cos (180^{o}-45^{o}) = -Cos45^{o} = -\frac{\sqrt{2} }{2}$

(Применили формулу приведения Cos(180° - α) = -Cosα)

$\displaystyle AC^{2} = 1^{2} +(3\sqrt{2} )^{2} -2*1*3\sqrt{2} *(-\frac{\sqrt{2} }{2}) =\\\\= 1 + 18 + 6 = 25 =5^{2}$

AC = 5 см.