Предмет: Математика,
автор: Angralfer
Вычислить пределы функции
Приложения:
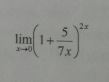
Ответы
Автор ответа:
0
Согласно второму замечательному пределу
получим
Если х стремится к нулю, то полученную неопределенность, используя экспоненциальное представление, раскрываем с помощью правила Лопиталя:
Похожие вопросы
Предмет: Английский язык,
автор: liliyaarakelyan1990a
Предмет: Физика,
автор: Sandroud
Предмет: Физика,
автор: dzhohan637
Предмет: Математика,
автор: ВоЛчЯ
Предмет: Алгебра,
автор: Аноним