Предмет: Геометрия,
автор: misterloria
На стороне PQ треугольника PQR взята точка N, а на стороне PR – точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит отрезок QL в отношении m:n, считая от точки Q. Найдите отношение PN:PR.
Ответы
Автор ответа:
5
Ответ:
Объяснение:
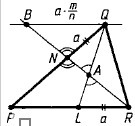
Пусть QL и NR пересекаются в одной точке - A.
NQ=LR=a
Через точку Q проведём прямую, которая параллельна PR. Пусть эта прямая будет пересекаться с прямой NR в точке B. Из подобия треугольников BAQ и RAL следует, что
Из этого подобия треугольников BNQ и RNP находим, что
Приложения:
misterloria:
большое спасибо
Похожие вопросы
Предмет: Алгебра,
автор: aleksashenka200988
Предмет: История,
автор: MolodoyMillionner
Предмет: Английский язык,
автор: mary90stell
Предмет: География,
автор: dinusja14
Предмет: Математика,
автор: Maxkas