Предмет: Алгебра,
автор: volkk822
найдите ординату вершины параболы график которой пересекает ось ординат в точке с ординатой 1, симметричен относительно прямой х+2=0 и проходит через точку (2;7)
Ответы
Автор ответа:
5
Уравнение параболы у= ах² + вх + с.
Один параметр вытекает из задания: параметр "с" равен ординате точки пересечения оси Оу: с = 1.
Далее используем формулу определения абсциссы вершины параболы: хо = -в/2а,
-2 = -в/2а, отсюда в = 4а.
Теперь используем данные точки (2; 7).
7 = а*2² + (4а)*2 + 1,
12а = 6,
а = 6/12 = 1/2, в = 4а = 4*(1/2).
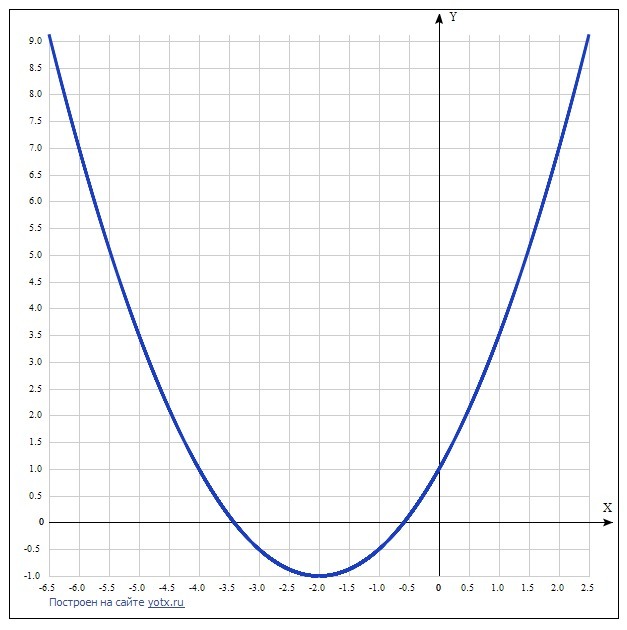
Получаем уравнение параболы у = (1/2)х² + 2х + 1.
Подставим абсциссу вершины хо = -2 и найдём её ординату:
уо = (1/2)*(-2)² + 2*(-2) + 1 = 2 - 4 + 1 = -1.
Ответ: уо = -1.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: hrumsuper
Предмет: Алгебра,
автор: kewok
Предмет: Русский язык,
автор: askarbaevdiar50
Предмет: Математика,
автор: varyuhin
Предмет: Алгебра,
автор: ОпытныйФизик