Question

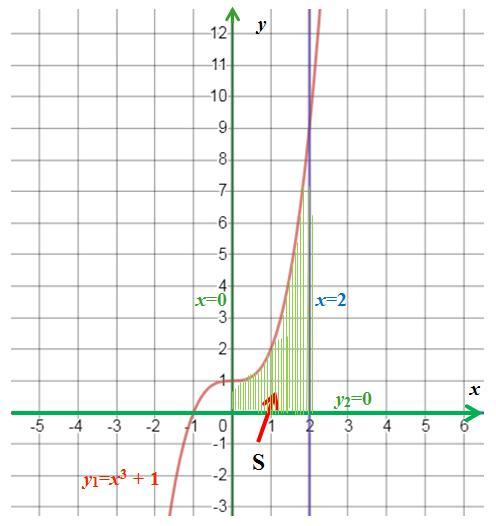
9 Вычислите площадь фигуры (S), ограниченной линиями у = х3 + 1, у = 0, х = 0, х = 2.
Вычислите площадь фигуры (S), ограниченной линиями у = 4 –х2, у = 0, х = 0, х = 2.
Решите пожалуйста, нужен только ответ.

Answer 1

Ответ:

6 (кв. единиц)

Пошаговое объяснение:

Фигура ограничена: сверху  функцией y₁=x3+1, слева x=0, справа x=2, снизу прямой y₂=0 (см. рисунок). Площадь S фигуры вычислим с помощью определенного интеграла:

$\displaystyle S=\int\limits^ {2}_{0} {(y_{1}-y_{2} )} \, dx =\int\limits^ {2}_{0} {(x^{3} +1-0)} \, dx =\int\limits^ {2}_{0}(x^{3}+1) \, dx = (\frac{1}{4} \cdot x^{4}+x) \left | {^{2}_{0}} \right.=\\\\=(\frac{1}{4}\cdot 2^{4}+2)-(\frac{1}{4}\cdot 0^{4}+0)=(\frac{16}{4}+2) -0=4+2=6$