Предмет: Геометрия,
автор: mirinka27071999
Помогите пожалуйста. Очень нужно
Номер 4 ( обязательно) и 5 ( не обзательно)
Ответы
Автор ответа:
0
Задача 4
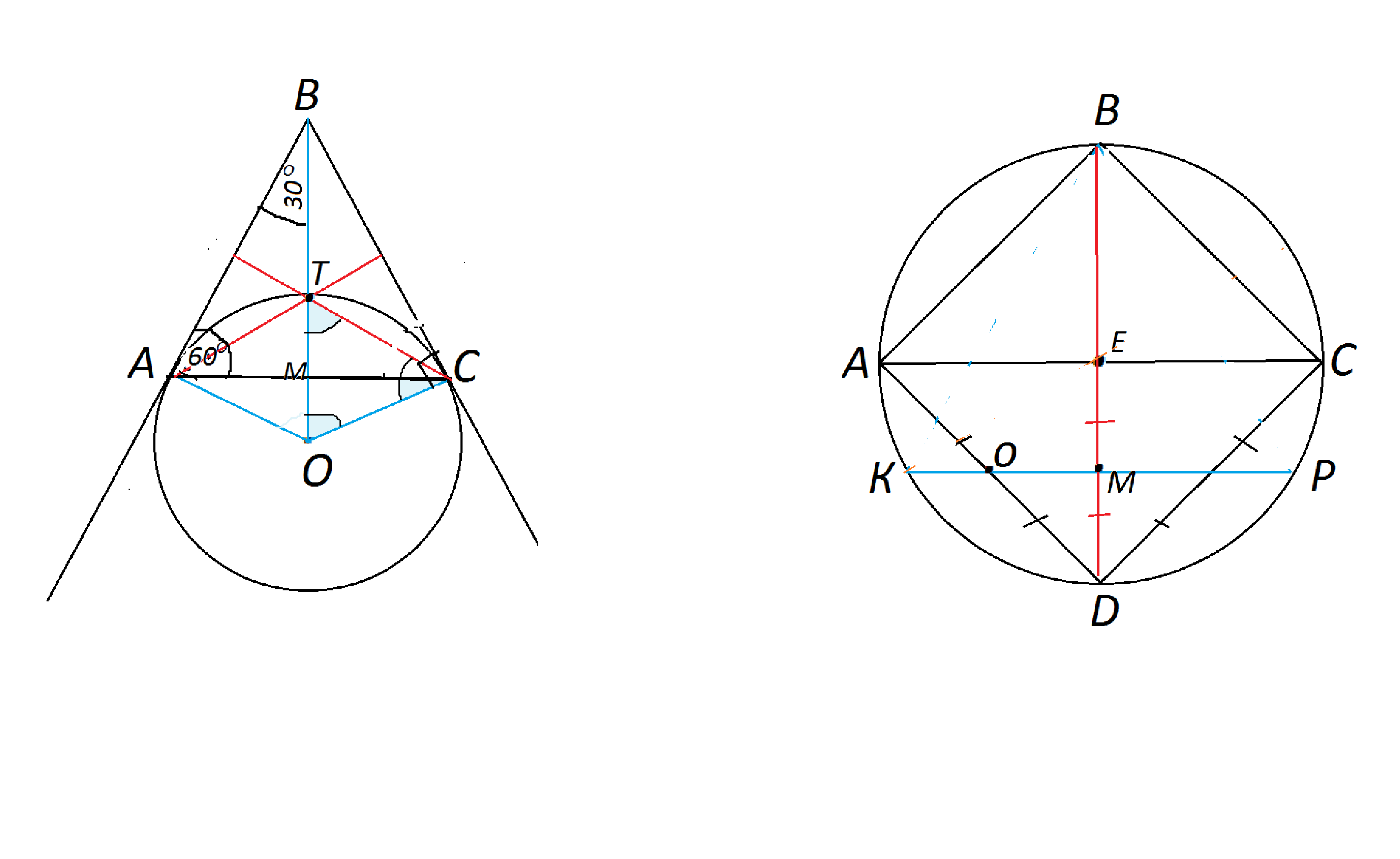
К окружности с центром в точке О проведены из точки В касательные АВ и ВС (А и С - точки касания), Окружность пересекает отрезок ОВ в точке Т. ∠АВТ=30°. Доказать, что Т - точка пересечения биссектрис ∆ АВС.
----------------------------------------------------
Нарисуем окружность и касательные ВА и ВС.
Соединим А и С с центром окружности и с точкой В.
АВ=ВС как отрезки касательных из одной точки,
АО=ОС - радиусы,
ОВ - общая сторона.
∠ОВС=∠АВО=30°.
Точка Т лежит на ВО
ВО - гипотенуза треугольника, в котором
катет, противолежащий углу 30°, равен R.
ОТ - радиус => ВТ=ОТ.
Проведем АК и СР через точку Т до пересечения с АВ и АС.
Треугольники АОТ и ТОС образованы радиусами, они равнобедренные и равносторонние, так как центральные углы в них являются и углами прямоугольных треугольников, в которых один из острых углов ( при В) равен 30°.
Следовательно, центральные углы АОТ и ТОС равны 60°.
АС диагональ ромба и является биссектрисой углов ромба АОСТ.=>
∠ ТАС=∠ТСА=30° и отсюда СР и АК - биссектрисы углов А и С.
Но и ВМ биссектриса треугольника АВС.
Точка Т является точкой пересечения биссектрис треугольника АВС.
==================================================================
Задача 5
Вершины А, В, С и Д куба АВСДА₁В₁С₁D₁ лежат на окружности. Точкa О - середина ребра АD. Хорда окружности проходит через точку О и параллельна отрезку АС . Вычислить длину этой хорды, если площадь поверхности куба равна 384 см²
---------------------------------------
Обозначим концы хорды К и Р
Проведем в окружности диаметр ВD, который является хордой и диагональю вписанного квадрата.
Хорда КР делит диаметр на две части ВМ и МD.
Так как КР содержит среднюю линию треугольника АDС,
высота треугольника=радиус ЕD разделен в точке М пополам.
MD=1/4 диаметра окружности,
ВМ=3/4 диаметра
Произведения отрезков каждой хорды, получившихся при пересечении этих хорд, равны.
Диагонали квадрата при пересечении делятся пополам и перпендикулярны друг другу.
Хорда параллельна диаметру.
Диаметр делит хорду, к которой он перпендикулярен, пополам.
Пусть КМ=МР=х
Тогда х²=1/4 D×3/4 D=(3/16)D
х=0,25√3 D
КР=2х=0,5√3 D
Длина диаметра окружности равна диагонали грани куба.
Ребро куба найдем из площади его поверхности.
Граней у куба 6, площадь каждой а²=384:6=64см²
Ребро куба равно а= √64=8см
Диагональ грани равна 8√2см (d=a√2 )
Длина хорды КР=(0,5√3)×8√2= 4√6 см
К окружности с центром в точке О проведены из точки В касательные АВ и ВС (А и С - точки касания), Окружность пересекает отрезок ОВ в точке Т. ∠АВТ=30°. Доказать, что Т - точка пересечения биссектрис ∆ АВС.
----------------------------------------------------
Нарисуем окружность и касательные ВА и ВС.
Соединим А и С с центром окружности и с точкой В.
АВ=ВС как отрезки касательных из одной точки,
АО=ОС - радиусы,
ОВ - общая сторона.
∠ОВС=∠АВО=30°.
Точка Т лежит на ВО
ВО - гипотенуза треугольника, в котором
катет, противолежащий углу 30°, равен R.
ОТ - радиус => ВТ=ОТ.
Проведем АК и СР через точку Т до пересечения с АВ и АС.
Треугольники АОТ и ТОС образованы радиусами, они равнобедренные и равносторонние, так как центральные углы в них являются и углами прямоугольных треугольников, в которых один из острых углов ( при В) равен 30°.
Следовательно, центральные углы АОТ и ТОС равны 60°.
АС диагональ ромба и является биссектрисой углов ромба АОСТ.=>
∠ ТАС=∠ТСА=30° и отсюда СР и АК - биссектрисы углов А и С.
Но и ВМ биссектриса треугольника АВС.
Точка Т является точкой пересечения биссектрис треугольника АВС.
==================================================================
Задача 5
Вершины А, В, С и Д куба АВСДА₁В₁С₁D₁ лежат на окружности. Точкa О - середина ребра АD. Хорда окружности проходит через точку О и параллельна отрезку АС . Вычислить длину этой хорды, если площадь поверхности куба равна 384 см²
---------------------------------------
Обозначим концы хорды К и Р
Проведем в окружности диаметр ВD, который является хордой и диагональю вписанного квадрата.
Хорда КР делит диаметр на две части ВМ и МD.
Так как КР содержит среднюю линию треугольника АDС,
высота треугольника=радиус ЕD разделен в точке М пополам.
MD=1/4 диаметра окружности,
ВМ=3/4 диаметра
Произведения отрезков каждой хорды, получившихся при пересечении этих хорд, равны.
Диагонали квадрата при пересечении делятся пополам и перпендикулярны друг другу.
Хорда параллельна диаметру.
Диаметр делит хорду, к которой он перпендикулярен, пополам.
Пусть КМ=МР=х
Тогда х²=1/4 D×3/4 D=(3/16)D
х=0,25√3 D
КР=2х=0,5√3 D
Длина диаметра окружности равна диагонали грани куба.
Ребро куба найдем из площади его поверхности.
Граней у куба 6, площадь каждой а²=384:6=64см²
Ребро куба равно а= √64=8см
Диагональ грани равна 8√2см (d=a√2 )
Длина хорды КР=(0,5√3)×8√2= 4√6 см
Приложения:
Похожие вопросы
Предмет: Физкультура и спорт,
автор: kcicesplay
Предмет: Английский язык,
автор: sempaigovno
Предмет: История,
автор: MishinaPolina1234567
Предмет: История,
автор: alice123456789
Предмет: Химия,
автор: ybry