Предмет: Геометрия,
автор: TheStrike666
Основания трапеции равны 16 см и 41 см. Найти площадь этой трапеции, если боковые стороны равны 15 см и 20 см.
Ответы
Автор ответа:
3
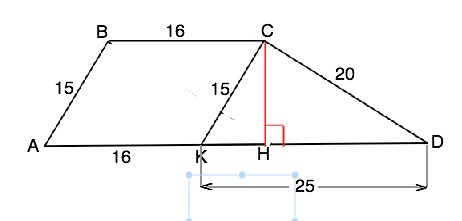
Обозначим вершины трапеции АВСD. Стороны: АВ=15, ВС=16, СD=20, AD=41. Из вершины С проведем СК параллельно АВ. Тогда АВСК - параллелограмм, и СК=15 см, АК=ВС=16 см, КD=AD-AK=25 см. Отношение сторон ∆ СКD=15:20:25, т.е. 3:4:5. ⇒ ∆ КСD - так называемый египетский, он прямоугольный. Площадь ∆ КСD=KC•CD:2=150 см². Тогда его высота СН=2S:KD=300:25=12 см (она же высота трапеции АВСD). Площадь трапеции равна половине произведения высоты на сумму оснований. S(ABCD)=CH•(BC+AD):2=12•57:2=342 см²
Подобных задач с полным и правильным ответом на сайте немало. При желании можно найти другие варианты решения.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: klwgii
Предмет: Алгебра,
автор: kartonkadyd
Предмет: Физика,
автор: gulnora1984
Предмет: Математика,
автор: Аноним