Предмет: Геометрия,
автор: Coolgirl290703
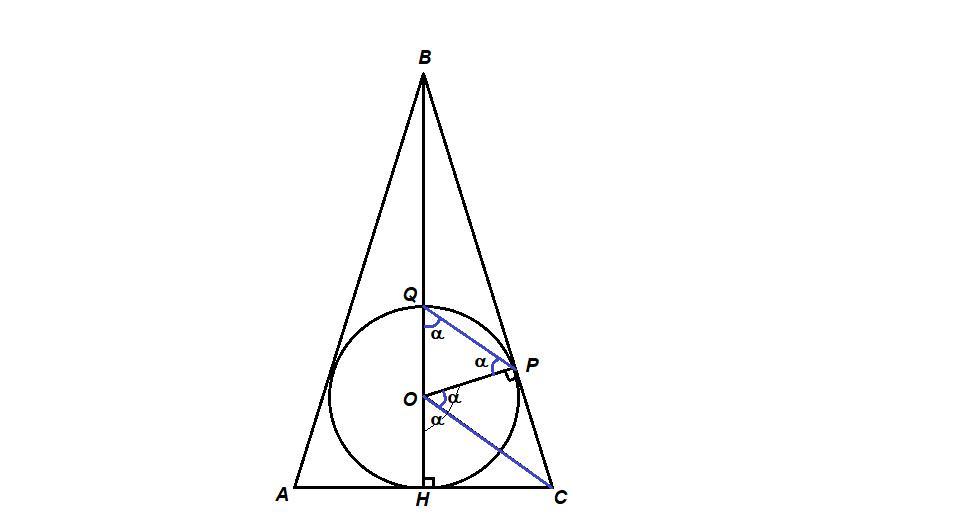
Дан равнобедренный треугольник АВС с основанием АС. Вписанная в него окружность
с центром О касается боковой стороны ВС в точке Р и пересекает биссектрису угла В в точке Q.
Докажите, что отрезки QP и ОС параллельны.
Ответы
Автор ответа:
2
Ответ:
ВН - биссектриса равнобедренного треугольника, проведенная к основанию, значит ВН - высота.
ОР⊥ВС как радиус, проведенный в точку касания.
ΔOPQ равнобедренный (OP = OQ как радиусы), значит
∠OPQ = ∠OQP = α
∠POH = ∠OPQ + ∠OQP = 2α как внешний угол треугольника OPQ.
ΔСОН = ΔСОР по катету и гипотенузе (∠СНО = ∠СРО = 90°, ОН = ОР как радиусы, ОС - общая), значит
∠СОР = ∠СОН = 1/2 ∠РОН = α.
Итак, ∠OPQ = ∠COP = α, а эти углы - внутренние накрест лежащие при пересечении прямых QP и ОС секущей ОР, значит
QP ║ OC.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: arachan2505
Предмет: История,
автор: burapolina2020
Предмет: Другие предметы,
автор: zarminakomilzonova
Предмет: История,
автор: Anuta324
Предмет: Математика,
автор: GoodMan12