Question

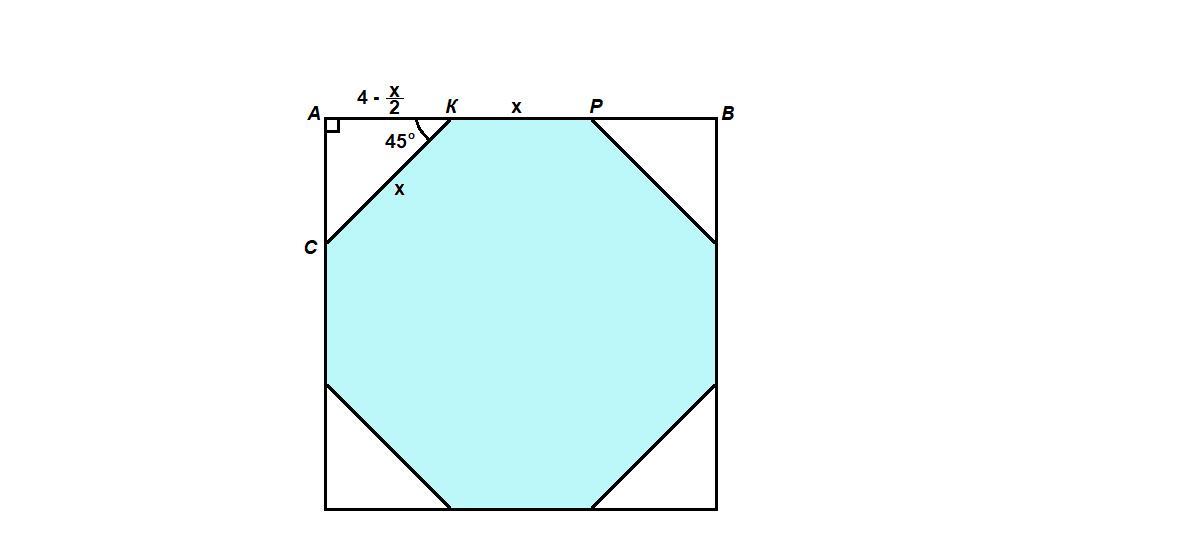
Углы квадрата со стороной 8 см срезали так, что получили правильный восьмиугольник. Найдите сторону полученного восьмиугольника

Answer 1

Ответ:

(8√2 - 8) см

Объяснение:

Пусть х - сторона восьмиугольника.

Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360°. Найдем внешний угол восьмиугольника:

360° : 8 = 45°

Срезанные углы квадрата - равные прямоугольные треугольники, а так как острые углы у них по 45°, то они равнобедренные.

$AK=PB=\dfrac{AB-KP}{2}=\dfrac{8-x}{2}=4-\dfrac{x}{2}$

Из прямоугольного треугольника АСК по теореме Пифагора составим уравнение:

АС² + AK² = CK²

2AK² = CK²

$2\cdot \Big(4-\dfrac{x}{2}\Big)^{2}=x^{2}$

$2\cdot \Big(16-4x+\dfrac{x^{2}}{4}\Big)=x^{2}$

$32-8x+\dfrac{x^{2}}{2}=x^{2}$

$64-16x+x^{2}=2x^{2}$

$x^{2}+16x-64=0$

$\dfrac{D}{4}=\Big(\dfrac{b}{2}\Big)^{2}-ac=8^{2}+64=128$

$\sqrt{128}=8\sqrt{2}$

$x=\dfrac{-\frac{b}{2}\pm \sqrt{\frac{D}{4}}}{a}$

$x=-8-8\sqrt{2}$  не подходит по смыслу задачи,

$x=-8+8\sqrt{2}=8\sqrt{2}-8$ см