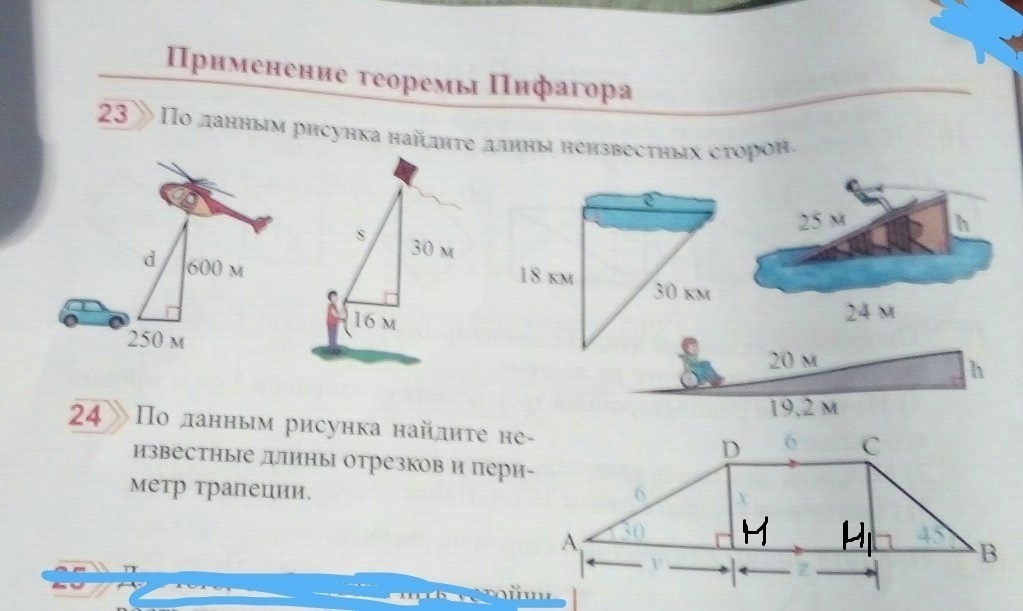
помогите пожалуйста!!! Даю 20 баллов!!! Прошу!!! N23 и N24.
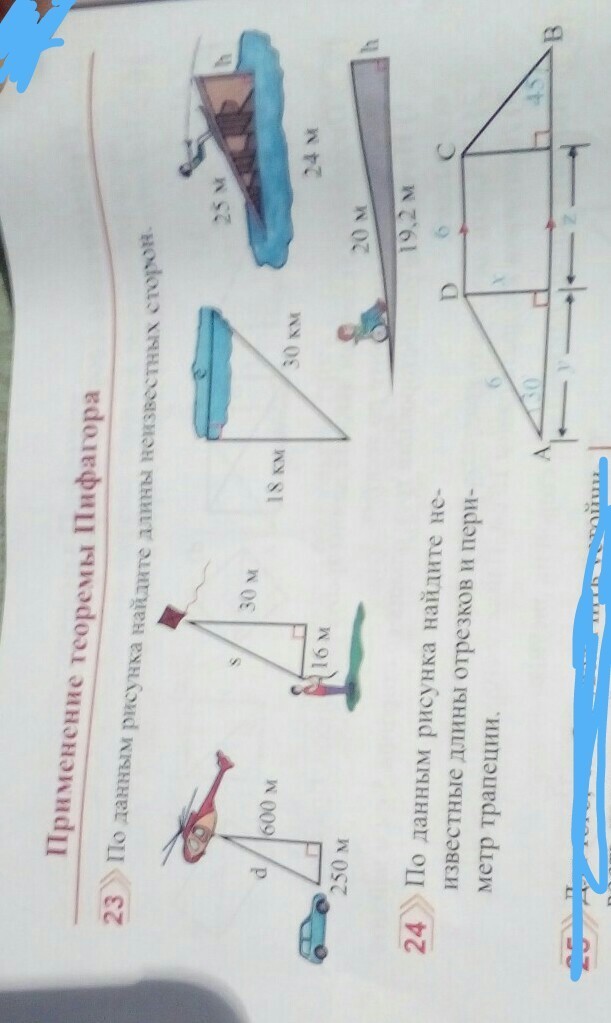
Ответы
Ответ:
23(1): d=650 (м)
23(2): s=34(м)
23(3): 24 (км)
23(4): h=7 (м)
24: x=3
y=5
z=6
P(ABCD)=26+3sqrt(2)
Пошаговое объяснение:
N23(1)
Т.к. d - гипотенуза, она расп. напротив угла в 90*, то применим т. Пифагора:
a^2=b^2+c^2
d^2= 250^2+600^2
d^2=62500+360000
d^2=422500
d=sqrt(422500)=650, отриц знач. не подх., т.к. длина чего либо>0
(2)
Т.к. s - гипотенуза, она расп. напротив угла в 90*, то применим т. Пифагора:
s^2=16^+30^2
s^2=256+900
s^=1156
s=sqrt(1156)=34, отриц знач. не подх., т.к. длина чего либо>0
(3)
Здесь гипотенузой явл. отрезок длиной = 30 км, а неизвест. катет = e => применим т. Пифагора:
a^2=b^2+c^2; b^2=a^2-c^2
e^2=30^2-18^2
e^2=576
e=sqrt(576)=24, отриц знач. не подх., т.к. длина чего либо>0
(4)
Здесь гипотенузой явл. отрезок длиной = 25 м, а неизвест. катет = h => применим т. Пифагора:
1-ый способ:
25, 24, 7 - "пифагорова тройка"
т.е. этот способ устный
2-ой способ:
a^2=b^2+c^2; b^2=a^2-c^2
h^2=25^-24^2
h^=49
h=sqrt(49)=7, отриц знач. не подх., т.к. длина чего либо>0
(5)
Здесь гипотенузой явл. отрезок длиной = 20 м, а неизвест. катет = h => применим т. Пифагора:
a^2=b^2+c^2; b^2=a^2-c^2
h^2=20^2-19,2^2
19,2^2 тоже самое что и 192^2, только здесь мы запятой 2 знака справа отделим.
h^2=31,36
h=5,6 отриц знач. не подх., т.к. длина чего либо>0
N25
Дано:
ABCD-трапец.
AD=6
DC=6
<A=30*
<B=45*
Найти:
y=?
x=?
z=?
P(ABCD)=?
Решение:
1) Обозначим высоты, как DH и CH1 соответственно
2)Рассм. треугол. ADH
а) <H=90* => треугол. - прямоугл. <A=30* =>
=> Либо: по определ. синуса DH=6*sin30*=6*1/2=3
=> Либо: по т. о том, что в прямоугл. треугол. против угла в 30* лежит катет в 2 раза меньше гипотенузы => DH=1/2*AD=6*1/2=3
б) y(AH)- катет => применим т. Пифагора:
a^2=b^2+c^2; b^2=a^2-c^2
y^2=6^-3^2
y^=36-9=25
y=sqrt(25)=5, отриц знач. не подх., т.к. длина чего либо>0
AH=y=5
2)Рассм. фигуру DCHH1 - это прямоугольник, т.к. DC II HH1 , т.к.
а) основ. трапеции параллельны,а HH1 как раз лежит на отрезке(или прямой) AB
б) DH II CH1, т.к. это высоты(по т. о двух прямых перпендикулярных третьей)
в) <D=<H=<H1=<C=90*
Вывод: противоположн. стороны прямоугол. равны =>
=> DC=HH1=z=6
=> CH1=DH=x=3
3)Для нахожд. P(ABCD) нам нужен "кусок" от АB, т.е. H1B
4) Рассм. треугол CH1B, в котором <CH1B=<CH1A по св-ву смеж углов => треугл. CH1B - прямоугл.
а) т.к. <B=45* =>
=> Либо: <C=180*-90*-45*=45*=<B
=> Либо: <C=90*-45*=45*=<B, т.к. трегол. СH1B - прямоугл.
б) Значит, треугол. CH1B -р/б по признаку =>СH1=H1B=3
в) По т. Пифагора
СB^= (CH1)^2+(H1B)^2=3^+3^2=18
CB=sqrt(18)=sqrt(9*2)=3sqrt(2), отриц знач. не подх., т.к. длина чего либо>0
5)AB=AH+HH1+H1B=y+z+x=5+6+3=14
6)P(ABCD)=AD+DC+CB+AB=6+6+3sqrt(2)+14=26+3sqrt(2)