Question

Помогите даю 50 баллов.Геометрия .в параллелограмме abcd угол bad=30 градусов,bd=bc= 3√3 см.найдите площадь пераллелограмма

Answer 1

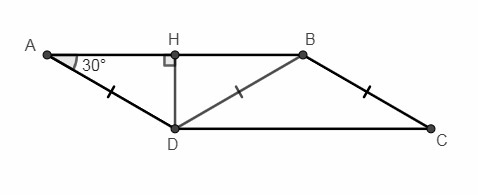
АВСD - параллелограмм
∠ВАD = 30°
ВD = ВС = 3√3 см
Найти: S.

Решение:
АD = ВС = 3√3  (свойство параллелограмма)
Опустим высоту ВН на сторону АВ.
В прямоугольном треугольнике катет, лежащий против угла 30° равен половине гипотенузы, отсюда:

$\tt DH=\cfrac{AD}{2} =\cfrac{3\sqrt{3}}{2}$  (см)

Найдем АН по теореме Пифагора:

$\tt AH=\sqrt{AD^2-DH^2}=\sqrt{(3\sqrt{3})^2-\left(\cfrac{3\sqrt{3}}{2}\right)^2} =\sqrt{27-\cfrac{27}{4}}=\sqrt{\cfrac{81}{4}}=\cfrac{9}{2}$  (см)

ΔАDВ равнобедренный, следовательно ВН является высотой и медианой, тогда $\tt AB=2AH=2\cdot\cfrac{9}{2}=9$  (cм)

Площадь параллелограмма равна произведению основания на высоту:

$\tt S_{ABCD}=AB\cdot DH=9\cdot\cfrac{3\sqrt{3}}{2}=\cfrac{27\sqrt{3}}{2}$  (см²)