Предмет: Алгебра,
автор: Dracon5449
Помогите!!!11!!1!!11!!!
Приложения:
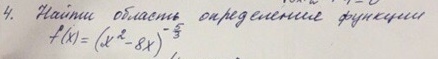
Ответы
Автор ответа:
0
Знаменатель дроби не должен равняться нулю, так как на ноль делить нельзя.
x² - 8x ≠ 0
x(x - 8) ≠ 0 ⇒ x ≠ 0 ; x ≠ 8
Область определения : все x ∈ ( - ∞ ; 0) ∪ (0 , 8) ∪ (8 ; + ∞)
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: kikkikov253
Предмет: Химия,
автор: musicbrawn
Предмет: Українська мова,
автор: kovalenkoyaroslav9
Предмет: Математика,
автор: тлаа
Предмет: Математика,
автор: bloodwork1