Предмет: Математика,
автор: denisevdokimov
Найти алгебраическую форму комплексного числа
Приложения:
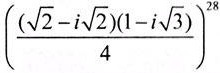
Ответы
Автор ответа:
0
Ответ:
r=
Z=r где
=
=
Z²⁸=1²⁸*
Похожие вопросы
Предмет: Математика,
автор: asarapova978
Предмет: Математика,
автор: kasenovandrej
Предмет: Қазақ тiлi,
автор: gesken610
Предмет: Математика,
автор: математика486