Предмет: Математика,
автор: mattserious2302
Помогите решить неравенство пожалуйста
Приложения:
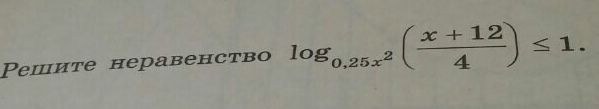
Ответы
Автор ответа:
1
Ответ: x ∈ (-12; -3] ∪ (-2; 2) ∪ [4; +∞)
Пошаговое объяснение:
ОДЗ
x ∈ (-12; -2) ∪ (-2; 2) ∪ (2; +∞)
Решаем уравнение в зависимости от значения основания логарифма (меньше или больше 1).
Если больше 1, то:
x ∈ (-∞; -3] ∪ [4; +∞)
С учетом ОДЗ x ∈ (-12; -3] ∪ [4; +∞)
Если меньше 1, то
x ∈ (-2; 2)
С учетом ОДЗ x ∈ (-2; 2)
Окончательное решение:
x ∈ (-12; -3] ∪ (-2; 2) ∪ [4; +∞)
mattserious2302:
Дай бог здоровья
Похожие вопросы
Предмет: Математика,
автор: Vishnekaaa
Предмет: Литература,
автор: nikitoskul777
Предмет: Математика,
автор: sofia726010
Предмет: Математика,
автор: мама588
Предмет: Математика,
автор: aika113