Предмет: Алгебра,
автор: bawib
ПОМОГИТЕ РЕШИТЬ ТРИГОНОМЕТРИЧЕСКОЕ УРАВНЕНИЕ ПОЖАЛУЙСТА!!!!
Приложения:
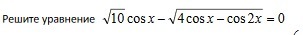
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: dairaserik28
Предмет: Геометрия,
автор: bupsipalte
Предмет: Химия,
автор: suiiiiiiiiiiiii
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Zhanelya555