Предмет: Алгебра,
автор: ClarisVerbis
Объясните, пожалуйста, почему >
Приложения:
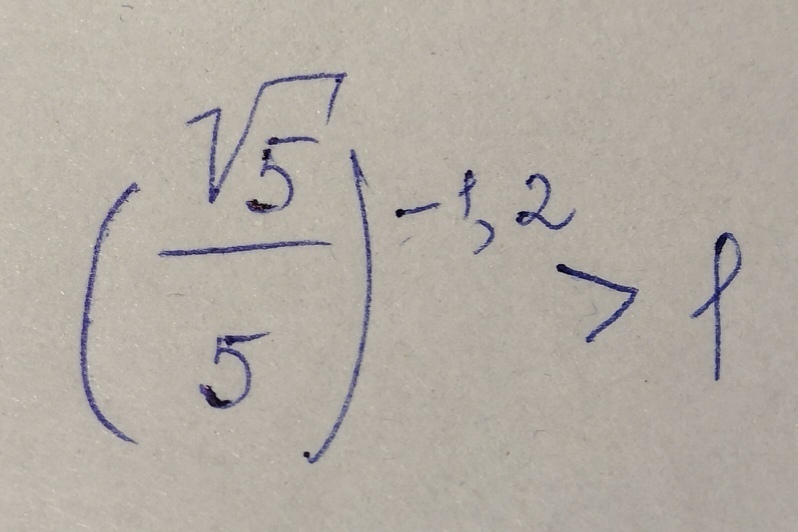
Ответы
Автор ответа:
1
рассмотрим число
уберем - из степень,для этого поменяем числитель со знаменателем местами
сокращаем
и так приблизительно равен 2,2, что больше 1
а вдобавок возводим 2,2 в 1,2
в итоге
≈ 2,5
а 2,5 >1
Автор ответа:
0
1) Упростим выражение в левой части неравенства:
2) Теперь неравенство выглядит так:
3) Любое число в нулевой степени равно 1, т.е. а⁰ = 1 , поэтому в правой части неравенства получим:
4) Исходное неравенство имеет вид:
Из двух степеней с одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
У нас:
основание √5>1
левый показатель больше правого 1,2 >0
значит, левая часть неравенства больше правой, т.е.
Доказано.
Похожие вопросы
Предмет: Физика,
автор: Alihan1019
Предмет: Алгебра,
автор: Tamerlan6082
Предмет: Химия,
автор: makanbaevsanzar
Предмет: География,
автор: Expertic
Предмет: Математика,
автор: 19761649