Предмет: Алгебра,
автор: d330991
Решите, пожалуйста.
Алгебра 10 класс
Приложения:
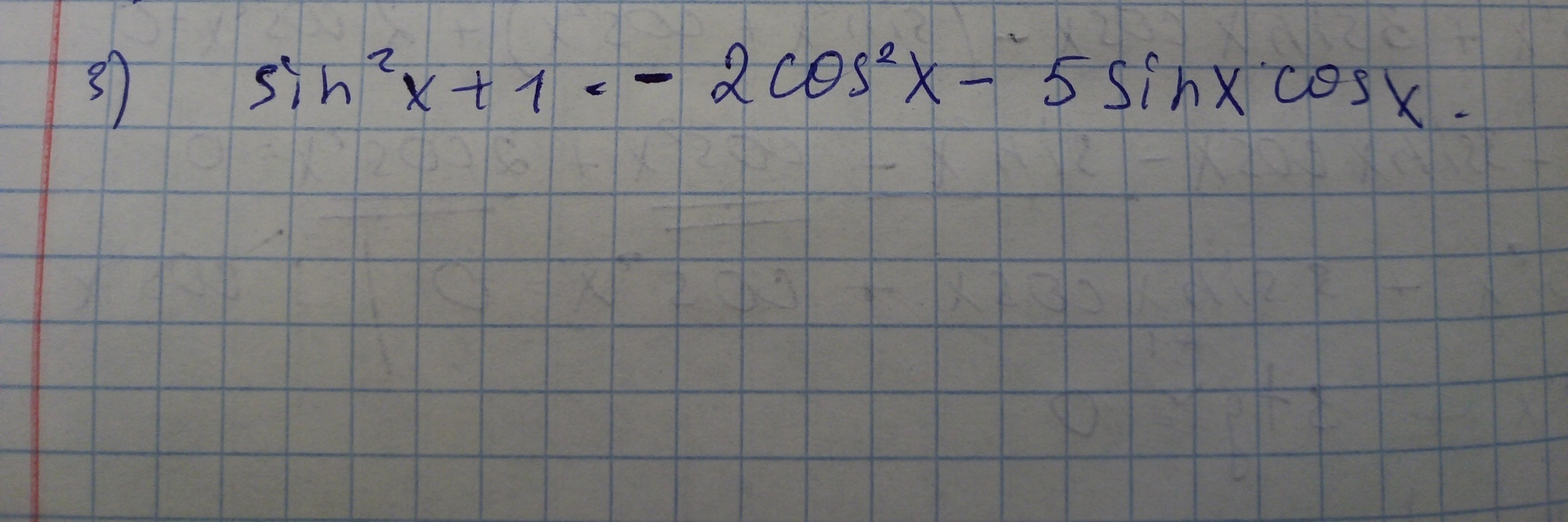
Ответы
Автор ответа:
0
sin²x + 1 = - 2cos²x - 5sinx•cosx
Применим основное тригонометрическое тождество: sin²x + cos²x = 1
sin²x + ( sin²x + cos²x ) = - 2cos²x - 5sinx•cosx
2sin²x + 5sinx•cosx + 3cos²x = 0
Однородное уравнение. Разделим обе части данного уравнения на cos²x ≠ 0 ⇒
2tg²x + 5tgx + 3 = 0
D = 5² - 4•2•3 = 25 - 24 = 1
tg₁x = ( - 5 - 1 )/4 = - 6/4 = - 3/2 ⇒ x = - arctg(3/2) + пn, n ∈ Z
tg₂x = ( - 5 + 1 )/4 = - 4/4 = - 1 ⇒ x = - п/4 + пk, k ∈ Z
ОТВЕТ: - arctg(3/2) + пn, n ∈ Z ; - п/4 + пk, k ∈ Z
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nf78vvt7q4
Предмет: Геометрия,
автор: YanaKuchukova
Предмет: Русский язык,
автор: inessapenova447
Предмет: Алгебра,
автор: ffffffthwhw
Предмет: История,
автор: AnastasiaLetova