Предмет: Алгебра,
автор: 111111DA
Найдите корень уравнения:
Тема:показательные уравнения
Приложения:
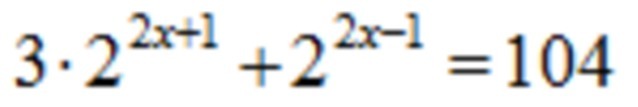

Ответы
Автор ответа:
4
Ответ: {2}
Так как множество значений показательной функции - числовой промежуток (0; ∞), то у₂ не удовлетворяет условию задачи.
Ответ: {4}
Похожие вопросы
Предмет: Обществознание,
автор: eisleep690
Предмет: Математика,
автор: zlatik1702
Предмет: Литература,
автор: Chelovek907
Предмет: Математика,
автор: Хачик19371