Предмет: Алгебра,
автор: dasew12
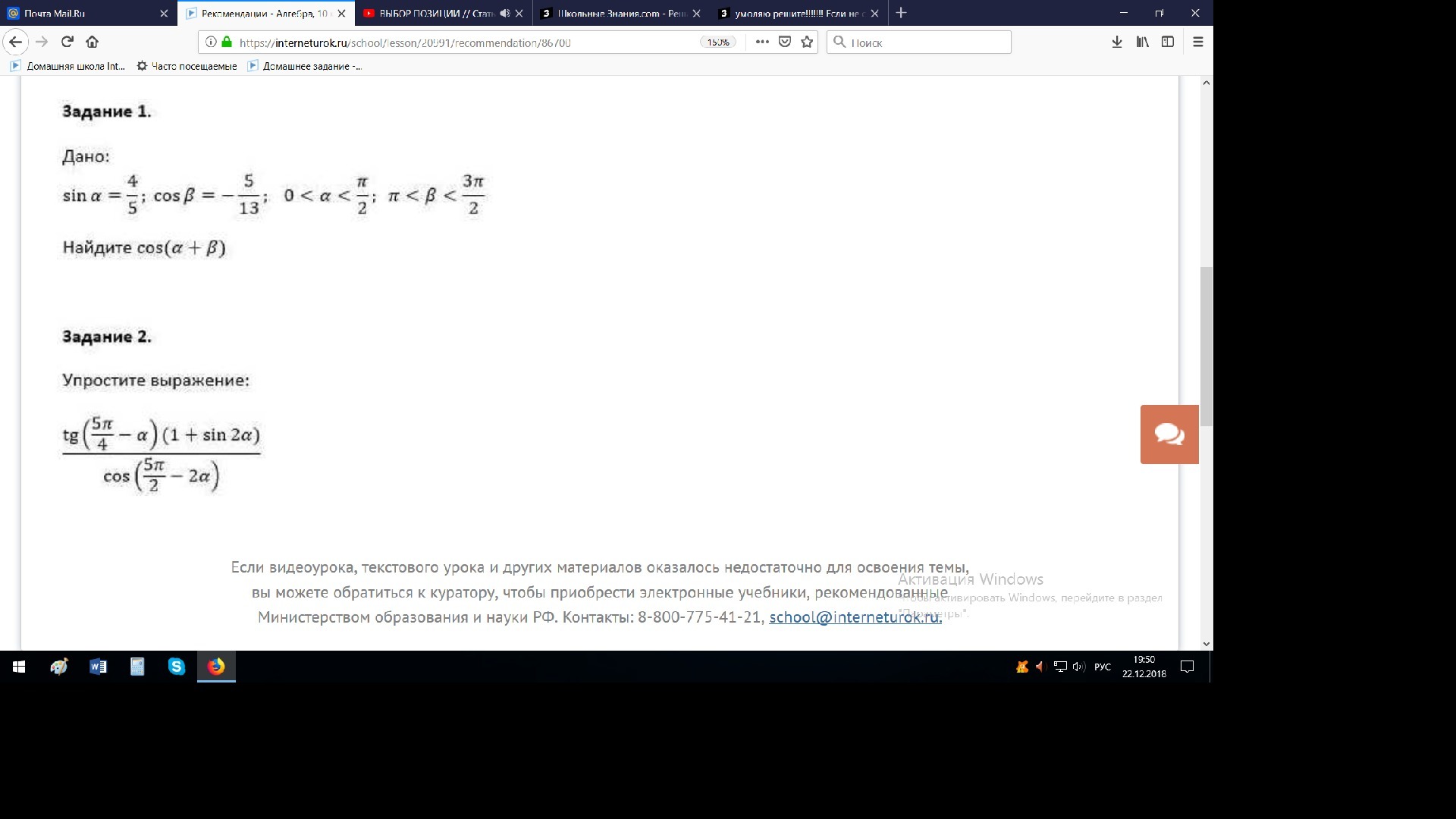
Помогите пожалуйста!"
Приложения:
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Обществознание,
автор: Alisahelloy
Предмет: Химия,
автор: Kaira23154
Предмет: Математика,
автор: XeII
Предмет: Математика,
автор: Виолетта0686
Предмет: Химия,
автор: ivanovanastya03