Предмет: Геометрия,
автор: NeZeRAvix
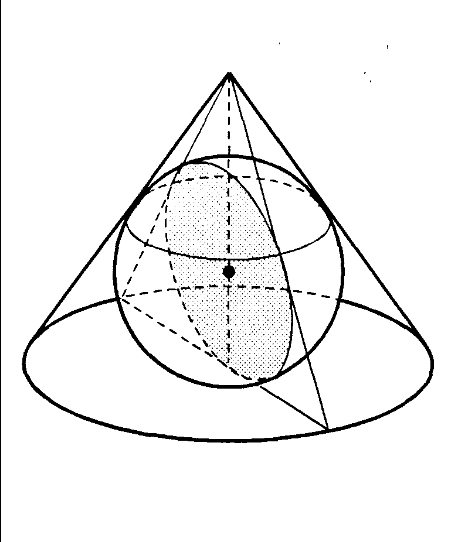
В конус вписан шар. Найдите угол между образующей конуса и плоскостью
основания конуса, если отношение объема конуса к объему
вписанного шара равно 9/4, а отношение радиуса шара к радиусу
основания конуса меньше 3/5.
Ответы
Автор ответа:
5
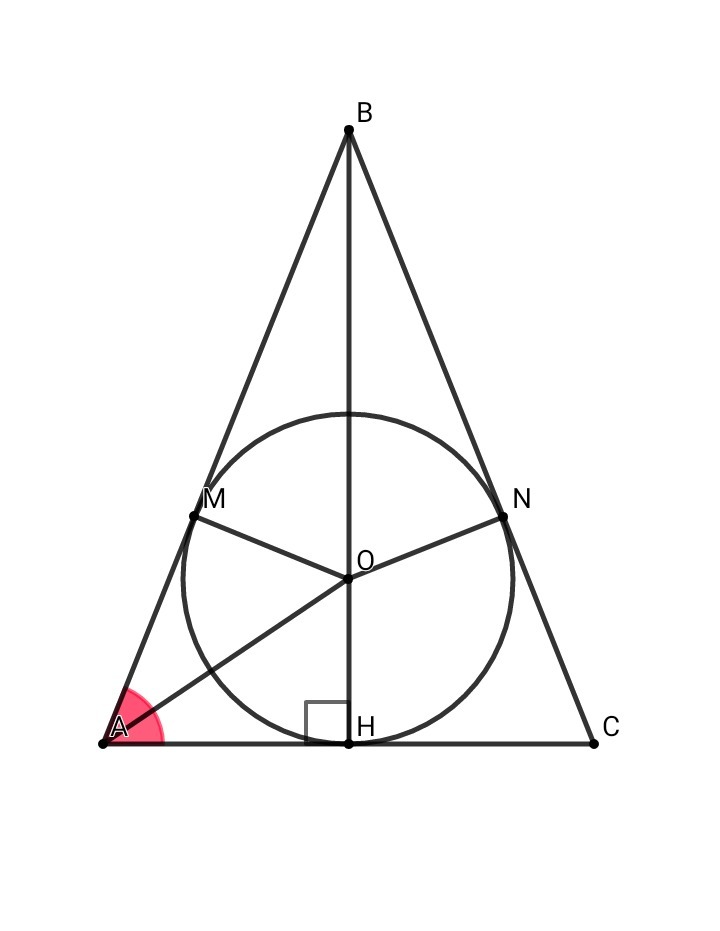
▪Рассмотрим Δ ABC - осевое сечение данного конуса ( равнобедренный треугольник ) , тогда точка O - центр вписанного шара , точка Н - центр основания конуса, ОН = OM = ON = r , AH = HC = R , ∠А = а - искомый угол между образующей и основанием конуса.
▪Точка О является центром вписанной окружности в Δ АВС ⇒ точка О - точка пересечения биссектрис ⇒ ∠ВАО = ∠НАО = а/2
▪В ΔAHB: BH = AH•tga = R•tga
B ΔHAO: OH = AH•tg(a/2) = R•tg(a/2)
▪ Vконуса = ( п•AH²•BH )/3 = ( пR²•R•tga )/3 = ( пR³tga )/3
Vшара = ( 4п•ОН³ )/3 = ( 4п•R³•tg³(a/2) )/3
▪ Vконуса / Vшара = tga / 4tg³(a/2) ; tga = 2tg(a/2) / 1 - tg²(a/2) ⇒ Vконуса / Vшара = 2tg(a/2) / 4tg³(a/2)•( 1 - tg²(a/2) ) = 1 / 2tg²(a/2) - 2tg⁴(a/2) = k
2k•tg⁴(a/2) - 2k•tg²(a/2) + 1 = 0
D = ( 2k )² - 4•2k = 4k² - 8k = 4•( k² - 2k )
4•( k² - 2k ) ≥ 0 ⇒ k ≥ 2
tg²(a/2) = ( 2k +- 2√(k² - 2k) )/4k = ( k +- √(k² - 2k) )/ 2k ⇒ k = 9/4 ⇒
tg₁²(a/2) = 2/3 ⇒ tg(a/2) = √(2/3) ≈ 0,82
tg₂²(a/2) = 1/3 ⇒ tg(a/2) = √(1/3) ≈ 0,58
Из условия следует, что tg(a/2) = r / R < 0,6 ⇒ tg(a/2) = √3/3 ⇒ a/2 = п/6 ⇒ а = п/3 = 60°
ΔАВС - равносторонний , AB = BC = AC ⇒ L = 2R = D , r = √3R/3
ОТВЕТ: 60°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: bebrik50
Предмет: Геометрия,
автор: vovadenisov000
Предмет: Английский язык,
автор: Katunchik68
Предмет: Математика,
автор: Marfa1986
Предмет: Химия,
автор: Mukaido