Предмет: Геометрия,
автор: ИринаШумная
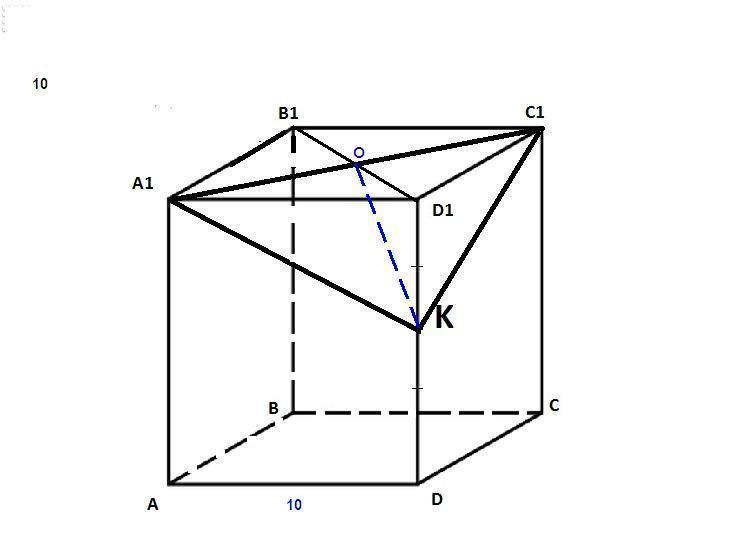
Дан куб abcda1b1c1d1, ребро которого равно 10. Найдите периметр и площадь сечения а1с1k1, если d1k=kd
Ответы
Автор ответа:
1
Не забудь отметить как лучшие пожалуйста!!!!!!!!!!!!!На самом деле это очень легко
Соединяем точки А₁, С₁ и К, так как они попарно лежат в одной грани.
А₁С₁ = 10√2 как диагональ квадрата.
ΔА₁D₁K: по теореме Пифагора
А₁К = √(A₁D₁² + D₁K²) = √(10² + 5²) = √125 = 5√5
ΔA₁D₁K = ΔC₁D₁K по двум катетам (A₁D₁ = C₁D₁ как ребра куба, D₁K - общий), значит А₁К = С₁К = 5√5
Рa₁c₁k = 10√2 + 5√5 + 5√5 = 10√2 + 10√5 = 10(√2 + √5).
КО - медиана и высота равнобедренного треугольника А₁С₁К.
По теореме Пифагора:
КО = √(А₁К² - А₁О²) = √(125 - (5√2)²) = √(125 - 50) = √75 = 5√3
Sa₁c₁k = 1/2 · A₁C₁ ·KO = 1/2 · 10√2 · 5√3 = 25√6
Приложения:
ИринаШумная:
У меня вообще никак с геометрией) Большое спасибо
пожалуйста обращайся но всё равно повтори или посмотри видео уроки тема очень важна!!!!!!!
Хорошо
Похожие вопросы
Предмет: Немецкий язык,
автор: Аноним
Предмет: Русский язык,
автор: osemlikoolssik
Предмет: Биология,
автор: sejitbeksema
Предмет: Математика,
автор: shadowkeish
Предмет: Математика,
автор: Cappuccinо