Question

У прямокутному трикутнику ABC (C= 90°) медіана AM перетинає висоту CD у точці K. Знайдіть відношення CK:KD якщо Кут BAC=60°.

Answer 1

Можно найти  точки пересечения прямой СД с прямыми АМ и АВ для получения координат точек К и Д.

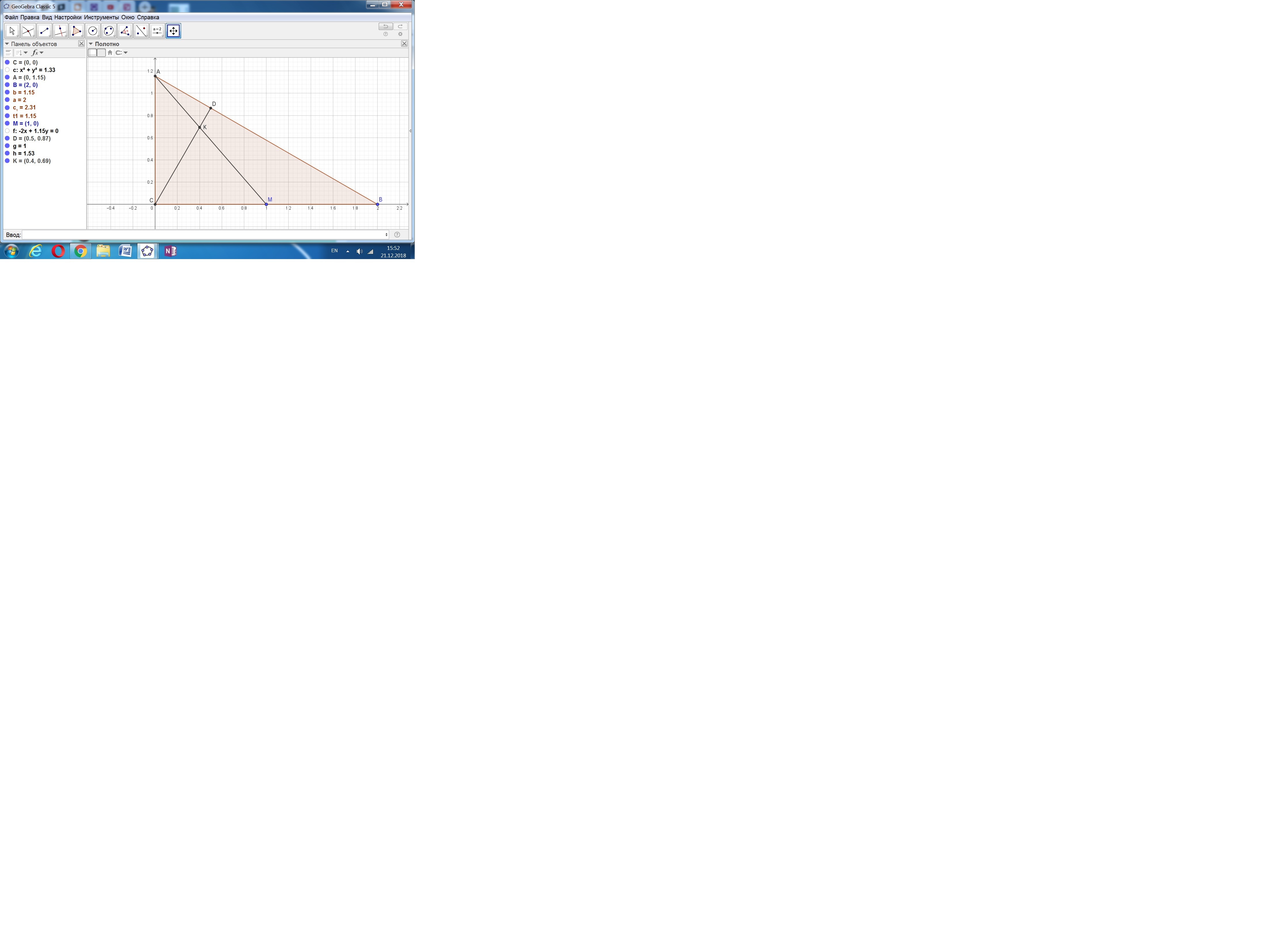
Пусть треугольник расположен в прямоугольной системе координат точкой С в начале, СВ по оси Ох.

Длину ВС примем равной 2 для удобства, АС = 2/√3.

Угловой коэффициент прямой СД равен √3, прямой АМ равен (-2/√3).

Точка К как пересечение СД и АМ: √3х = (-2/√3)х + (2/√3).

3х = -2х + 2,

5х = 2     х =2/5 = 0,4.

Точка Д как пересечение СД и АВ: √3х = (-1/√3)х + (2/√3).

3х = -1х + 2,

4х = 2     х =2/4 = 0,5.

Наклонные отрезки СК и СД пропорциональны их горизонтальным проекциям (это координаты по оси Ох).

Тогда СК:СД = 4/5.

Ответ: СК:КД = 4:1.